Условие задачи
Фирма принимает заказы на выполнение работ. Если в момент поступления заявки, хотя бы один мастер свободен, заявка принимается. В противном случае заказ теряется. Известно, что в среднем поступает λ заказов в час, среднее время обслуживания одного заказа составляет tобс часов. (При этом время поступления и время обслуживания заказов случайны и распределены экспоненциально.) Доход, получаемый фирмой в результате выполнения одного заказа, в среднем равен С ден. ед., а мастеру платят W ден. ед. в час. Требуется определить количество мастеров, при котором прибыль фирмы максимальна. Исходные данные:
- λ=3,20;
- tобс =0,63;
- С=7,83;
- W=2,68.
Ответ
Вначале найдем интенсивность нагрузки Р по формуле:
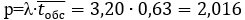(1)
Обозначим через n неизвестное количество мастеров.
Прибыль фирмы (n) зависит от числа мастеров п и находится по формуле:
(n) = Доход Расход (2)
При этом
Доход = А ∙ C (3)
где А - абсолютная пропускная способность.
Расход = n ∙ W (4)
Таким образом,
(n) = A∙C W∙ п ...
