Условие задачи
По 12 предприятиям исследовали зависимость У от Х, где Х – расходы на рекламу в СМИ, тыс. долл.; Y – прибыль предприятия, млн. долл. Признаки имеют нормальный закон распределения.
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между расходами на рекламу в СМИ и прибылью предприятия.
2. Рассчитайте оценки 
параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции (rв). Проверьте значимость коэффициента корреляции (α = 0,01).
4. Рассчитайте выборочный коэффициент детерминации (R2в). Сделайте экономический вывод.
5. Проверьте значимость оценки параметра с помощью критерия Стьюдента при уровне значимости α = 0,01.
6. Постройте 99-процентный доверительный интервал для коэффициента регрессии b. Сделайте экономический вывод.
7. Проверьте значимость оценки параметра с помощью критерия Стьюдента при уровне значимости α = 0,01.
8. Постройте 99-процентный доверительный интервал для свободного члена уравнения а.
9. Составьте таблицу дисперсионного анализа.
10. Оцените с помощью F-критерия Фишера - Снедекора значимость уравнения линейной регрессии (α = 0,01).
11. Рассчитайте прибыль предприятия (
), если расходы на рекламу будут равны 15 тыс. долл.. Постройте 99-процентный доверительный интервал для прогнозного значения объясняемой переменной (
). Сделайте экономический вывод.
12. Рассчитайте средний коэффициент эластичности (
). Сделайте экономический вывод.
13. Проверьте гипотезу Н0: b = b0, (b0 = 0,5).
14. На поле корреляции постройте линию регрессии.
Ответ
1. Построим поле корреляции (рис. 1) и сформулируем гипотезу о форме связи между признаками:
Х - расходы на рекламу в СМИ, тыс. долл.;
Y - прибыль предприятия, млн. долл.
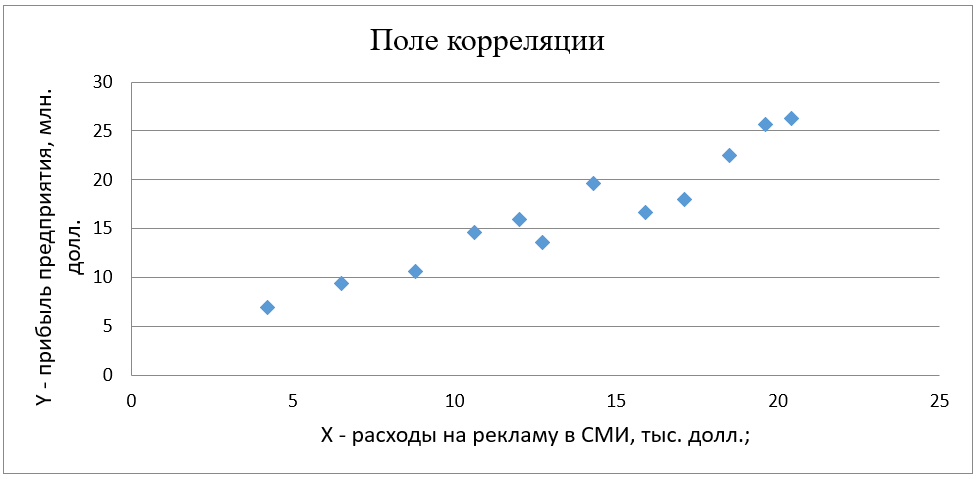
По расположению точек на поле корреляции можно предположить наличие прямой линейной связи между расходами на рекламу и прибылью предприятия.
2. Рассчитаем оценки параметров линейной модели
