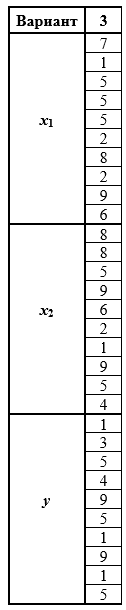
По результатам наблюдений найти точечные и интервальные оценки коэффициентов уравнения линейной регрессии у = β_0 + β_1 х_1 + β_2 х_2 и проверить общее качество уравнения линейной регрессии.
- Эконометрика
Условие:
По результатам наблюдений найти точечные и интервальные оценки коэффициентов уравнения линейной регрессии у = β0 + β1 х1 + β2 х2 и проверить общее качество уравнения линейной регрессии.
Все ли коэффициенты статистически значимы?
Проверить наличие гетероскедастичности с помощью теста ранговой корреляции Спирмена.
Определить наличие автокорреляции с помощью критерия Дарбина-Уотсона.
При наличии автокорреляции устранить её с помощью авторегрессионной схемы первого порядка AR(1).
Выяснить, есть ли в модели мультиколлинеарность.
Доверительная вероятность 0,95.
dl = 0,697; du = 1,641.
Решение:
1. Определим коэффициенты уравнения множественной линейной регрессии с двумя объясняющими переменными x1, x2 по методу наименьших квадратов. Промежуточные вычисления проведем в таблице 1:
Таблица 1
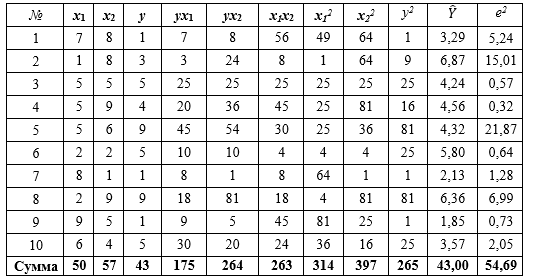
Для нахождения параметров линейного уравнения множественной регрессии:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства