Условие:
Проведено бюджетное обследование 27 случайно выбранных домохозяйств. Оно дало следующие результаты (в ден. ед.):
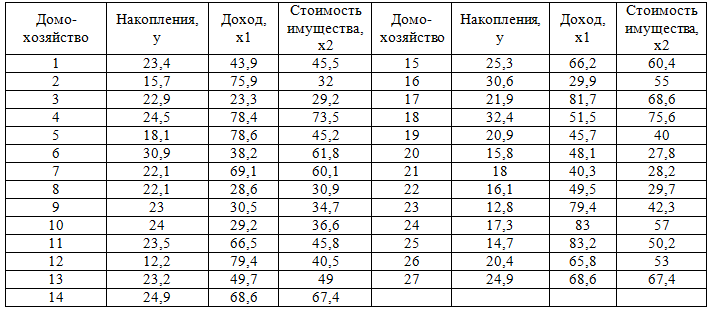
Требуется:
1. Построить корреляционное поле между накоплениями и доходом. Выдвинуть гипотезу о тесноте и виде зависимости между накоплениями и доходом.
2. Оценить тесноту линейной связи между накоплениями и доходом с надежностью 0,9.
3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости накоплений от дохода.
4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы.
5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9.
6. Для домохозяйства с доходом 59 ден. ед. дать точечный и интервальный прогноз накоплений с надежностью 0,9.
7. Рассчитать коэффициенты линейного уравнения множественной регрессии для зависимость накоплений от дохода и стоимости имущества. Пояснить экономический смысл его параметров.
8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.
9. Найти коэффициенты парной и частной корреляции. Проанализировать их.
10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
11. С помощью F-критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.
12. Для домохозяйства с доходом 59 ден. ед. и стоимостью имущества 38,6 ден. ед. дать точечный и интервальный прогноз накоплений с надежностью 0,9.
13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.
Решение:
1. Построим корреляционное поле между накоплениями и доходом.
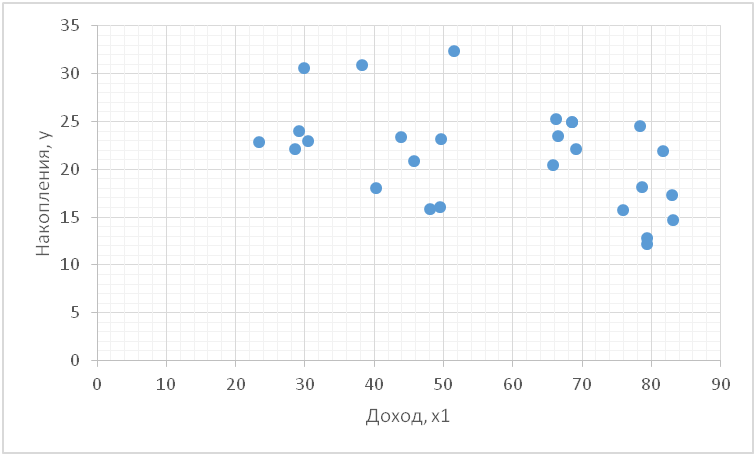
Рис. Поле корреляции
На основе анализа поля рассеяния выдвигаем гипотезу о том, что зависимость накоплений от стоимости имущества описывается линейной регрессионной моделью
