Условие:
1. Пусть для регрессии 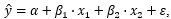 оцениваемой по ежегодным данным (1971-2008) получены следующие результаты: сумма квадратов остатков для данных 1971- 1981 гг. равна 15, для данных 1988-2008 гг. эта сумма равна 50. Проверьте предположение о том, что дисперсия отклонений не постоянна (в частности, что дисперсия претерпела изменение где-то в середине 80-х годов).
оцениваемой по ежегодным данным (1971-2008) получены следующие результаты: сумма квадратов остатков для данных 1971- 1981 гг. равна 15, для данных 1988-2008 гг. эта сумма равна 50. Проверьте предположение о том, что дисперсия отклонений не постоянна (в частности, что дисперсия претерпела изменение где-то в середине 80-х годов).
2. По 40 наблюдениям получена следующая модель производственной функции 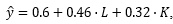 для которой R2 = 0.75, статистика Дарбина–Уотсона равна 2,35; t- статистика коэффициента при L равна 0,75, при K – 1,81, свободного слагаемого – 2,6. Здесь y, L, K – темпы прироста объема выпуска, затрат труда и капитала соответственно. Какие из следующих выводов представляются вам верными:
для которой R2 = 0.75, статистика Дарбина–Уотсона равна 2,35; t- статистика коэффициента при L равна 0,75, при K – 1,81, свободного слагаемого – 2,6. Здесь y, L, K – темпы прироста объема выпуска, затрат труда и капитала соответственно. Какие из следующих выводов представляются вам верными:
a) нужно ввести новую объясняющую переменную, так как доля объясненной дисперсии слишком мала;
b) имеет место автокорреляция остатков первого порядка, поэтому нужно изменить форму зависимости;
c) нужно исключить фактор L, так как он оказался статистически незначимым;
d) модель имеет удовлетворительные статистики, поэтому нет смысла ее совершенствовать.
Решение:
1. Выдвигается нулевая гипотеза 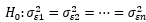 которая предполагает отсутствие гетероскедастичности.
которая предполагает отсутствие гетероскедастичности.
Для проверки этой гипотезы рассчитываем отношение которое имеет распределение Фишера с (k-m-1=10-2-1=7; 20-2-1=17) степеней свободы (здесь m число объясняющих переменных). Fтабл(0,05;7;17)=2,61
