Решить задачу распределения инвестиций методом динамического программирования. Задача распределения инвестиций: распределить В единиц средств среди n предприятий.
- Эконометрика
Условие:
Решить задачу распределения инвестиций методом динамического программирования
Задача распределения инвестиций: распределить В единиц средств среди n предприятий, доход gi(xj), i=1,2,…, n от которых в зависимости от количества вложенных средств xi , j=1,2,…,m задается матрицей (nxm+1) (дана в таблицах вариантов задания), таким образом, чтобы суммарный доход со всех предприятий был максимальным. Состояние системы перед каждым шагом определяется числом еще не распределенных средств.
Указание: разбить процесс оптимизации на n шагов так, чтобы на каждом k-м шаге оптимизировать инвестирование не всех предприятий, а только предприятий с k-го по n-ое. При этом считаем, что в остальные предприятия (с первого по (k-1)-ое) тоже вкладываются средства, и поэтому на инвестирование предприятий с k –го по n-ое остаются не все средства, а меньшая сумма ck ≤ B.
n=3, m=5
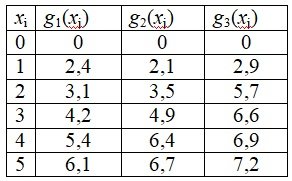
Решение:
I этап. Условная оптимизация.
1-ый шаг. k = 3.
Предположим, что все средства x3= 5 отданы предприятию №3. В этом случае, максимальная прибыль составит f3(u3) = 7,2, следовательно, F3(e3) = f3(u3)
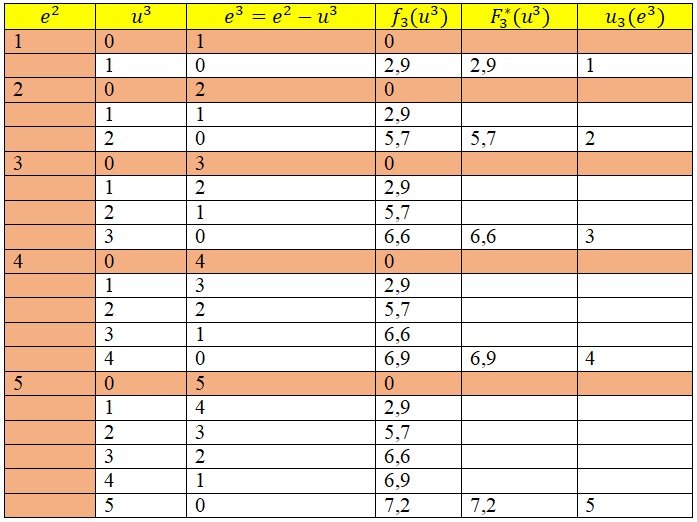
2-ый шаг. k = 2.
Найдем оптимальную стратегию при распределении денежных средств между предприятиями №2 и 3. Рекуррентное соотношение Беллмана имеет вид: F2(e2) = max(x2 e2)(f2(u2) + F2(e2-u...))
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства