Условие задачи
С целью определения средней суммы вкладов на 1 января текущего года в сберегательном банке, имеющем 2000 вкладчиков, по схеме собственно-случайной выборки с бесповторным отбором членов проведено обследование 200 лицевых счетов. Распределение вкладов по их величине (тыс. руб.) представлено в таблице:
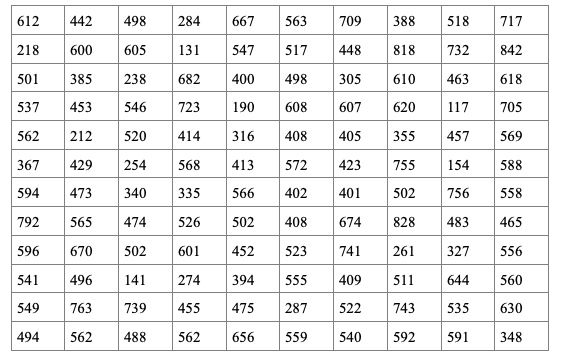
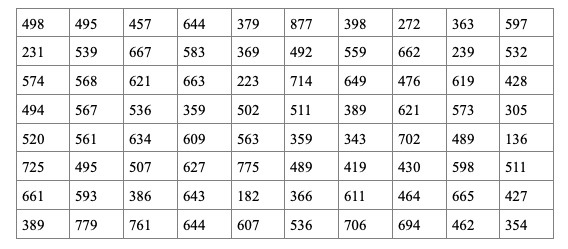
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот.
По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану.
Заменив параметры генеральной совокупности соответственно их наилучшими выборочными числовыми характеристиками и используя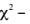 
критерий Пирсона, на уровне значимости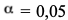 
проверить две гипотезы о том, что изучаемая случайная величина X – величина вклада – распределена:
а) по нормальному закону распределения;
б) по равномерному закону распределения.
Построить чертёж, на котором изображена гистограмма эмпирического распределения и соответствующие графики равномерного и нормального распределений.
Ответ
Решение.
Количество групп определим по формуле Стерджесса:
k=1+3,322lgN,
N число единиц совокупности.
k=1+3,322lg (200) =8,644=9 групп.
Ширину интервала определим по формуле:
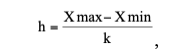
где хmax максимальное значение признака;
хmin минимальное значение признака;
k количество групп.
тыс. руб.
