Автомашина при ее эксплуатации может находиться в следующих состояниях: Х0 – исправна; Х1 – неисправна, проходит осмотр, который проводится с целью определения вида ремонта;
- Экономика предприятия
Условие:
Автомашина при ее эксплуатации может находиться в следующих состояниях:
Х0 – исправна;
Х1 – неисправна, проходит осмотр, который проводится с целью определения вида ремонта;
Х2 – неисправна, проходит капитальный ремонт;
Х3 – неисправна, проходит средний ремонт;
Х4 – неисправна, проходит текущий ремонт.
X5 – отремонтирована, проходит контроль и испытание на определение качества ремонта и выявление дефектов.
Среднее время межремонтного пробега равно t0 = 0,5 лет = 180 дней. Среднее время осмотра машины – t1 = 4 часа = 1/6 (0,167) дня. Вероятность qi каждого вида ремонта устанавливается исходя из уровня учета полного набора событий на интервале межкапитального ремонта в виде отношения количества ремонтов Ki каждого вида по всему количеству ремонтов в этом интервале, т.е
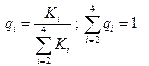
Длительность межкапитального интервала – tk = 5 лет, среднего tc = 2 года, текущего – t = 0.5 лет.
Среднее время ремонта равно t2 = 20 дн. – капитального; t3 = 7 дн. – среднего и t4 = 2 дн. – текущего.
После ремонта машина поступает на послеремонтный контроль. Качество ремонта определяется вероятностью d2 = 0.9 для капитального ремонта, d3 = 0,7 – среднего и d4 = 0.9 – текущего.
Изобразить график состояний системы с интенсивностями проходов из состояния в состояние. Определить вероятность нахождения машины в каждом из состояний, включая исправное состояние машины P0, а так же среднее время простоя машины.
Решение:
Поскольку время проведения контроля и испытаний не указано, считаем, что оно входит во время соответствующего вида ремонта. В результате граф состояний автомашины показан на рис.1.
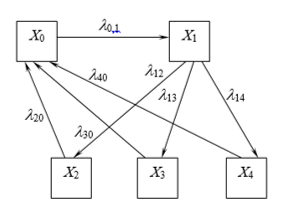
Рис. 1
В течение длительности межкапитального ремонта (5 лет) в среднем проводится 1 капитальный ремонт, 2,5 средних ремонтов (5 / 2) и 10 текущих (5 / 0,5) ремонтов, итого К = 1 + 2,5 + 10 = 13,5 ремонтов.
Вероятность каж...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства