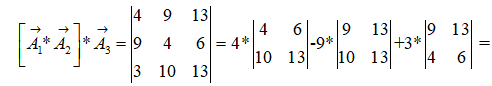Даны векторы A1, A2, A3, B ∈ R в кубе. Требуется: 1) доказать, что векторы A1, A2, A3 образуют базис пространства R в кубе. 2) разложить вектор B в этом базисе.
«Даны векторы A1, A2, A3, B ∈ R в кубе. Требуется: 1) доказать, что векторы A1, A2, A3 образуют базис пространства R в кубе. 2) разложить вектор B в этом базисе.»
- Экономика
Условие:
Даны векторы A1, A2, A3, B ∈ R3. Требуется:
1) доказать, что векторы A1, A2, A3 образуют базис пространства R3.
2) разложить вектор B в этом базисе.
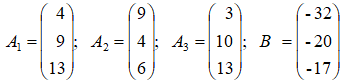
Решение:
1) Чтобы векторы A1, A2, A3 образовывали базис пространства R3, необходимо чтобы их смешанное произведение не было равно 0.
Смешанное произведение определитель матрицы, построенной на данных векторах:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э