Условие задачи
Обоснование оптимального плана производства
Организация имеет возможность выпускать три вида изделий П1, П2, П3, При их изготовлении используется три вида ресурсов Р1, Р2, Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами b1, b2, b3. Расход ресурса i-го вида (i=1,2,…,m) на единицу изделия j-го вида (j=1,2,…,n) составляет aijден. ед. Цена единицы продукции j-го вида равна сj.
Требуется найти оптимальный план выпуска изделий, который обеспечивал бы организации максимальный доход.
Обязательные требования к решению задачи.
1. Построить экономико-математическую модель задачи распределения ресурсов.
2. Построить двойственную задачу к задаче распределения ресурсов. Ввести соответствие переменных прямой и двойственной задачи.
3. Найти оптимальное решение прямой и двойственной задач линейного программирования двумя методамиА и Б, пояснить экономический смысл всех переменных, участвующих в решении.
4. Найти границы изменения дефицитных ресурсов, в пределах которых не изменится структура оптимального плана.
5. Уточнить значения недефицитных ресурсов, при которых оптимальный план не изменится.
6. Найти границы изменения цены изделия, попавших в оптимальный план производства, в пределах которых оптимальный план не изменится.
7. Определить величину ∆bs ресурса Рs, введением которого в производство можно компенсировать убыток и сохранить максимальный доход на прежнем уровне (ресурсы предполагаются взаимно заменяемыми), получаемый при исключении из производства ∆br единиц ресурса Рr.
8. Оценить целесообразность приобретения ∆bk единиц ресурса Рk по цене сk за единицу.
9. Установить, целесообразно ли выпускать новое изделие П4, на единицу которого ресурсы Р1, Р2, Р3 расходуются в количествах a14, a24, a34 единиц, а цена единицы изделия составляет с4денежных единиц.
10. Решить прямую и двойственную задачи линейного программирования в среде Microsoft Exсel, приложить отчеты.
Ответ
1. Обоснование оптимального плана производства
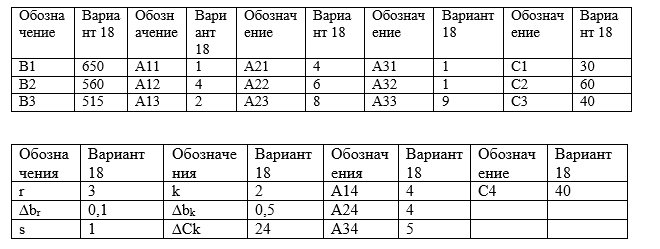
2. Построение экономико-математической модели задачи распределения ресурсов
Введем переменные:
х1 объем производства продукции первого вида;
х2 объем производства продукции второго вида;
х3 объем производства продукции третьего вида.
