1. Главная
  2. Библиотека
  3. Электроника, электротехника, радиотехника
  4. Длина кабеля равна l=2000 м, радиус токоведущей жилы r=7 мм и радиус оболочки R=42 мм. Изоляция кабеля имеет диэлектрическ...

Длина кабеля равна l=2000 м, радиус токоведущей жилы r=7 мм и радиус оболочки R=42 мм. Изоляция кабеля имеет диэлектрическую проницаемость εr=2,5.  Кабель рассчитан на напряжение U=154 кВ.

«Длина кабеля равна l=2000 м, радиус токоведущей жилы r=7 мм и радиус оболочки R=42 мм. Изоляция кабеля имеет диэлектрическую проницаемость εr=2,5.  Кабель рассчитан на напряжение U=154 кВ.»
  • Электроника, электротехника, радиотехника

Условие:

Задан одножильный маслонаполненный кабель с заземленной свинцовой оболочкой.

Длина кабеля равна l=2000 м, радиус токоведущей жилы r=7 мм и радиус оболочки R=42 мм. Изоляция кабеля имеет диэлектрическую проницаемость εr=2,5.  Кабель рассчитан на напряжение U=154 кВ. 

Требуется: 

1.  Рассчитать емкость кабеля. 

2.  Определить характер изменения напряженности электрического поля у поверхности токоведущей жилы при увеличении ее радиуса от r до R. 

3. Определить распределение потенциала в толще изоляции при неизменном радиусе внутренней жилы r. 

4.  Построить рассчитанные зависимости Ε=f (x), φ =f (x). 

Решение:

По теореме Гаусса напряженность электрического поля цилиндрического конденсатора в слое с радиусом rx равна:

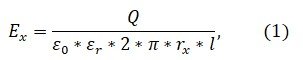
где Q заряд; 0=8,85*10-12 Фм диэлектрическая проницаемость вакуума; r относительная диэлектрическая проницаемость изоляции; rx расстояние от токоведущей жилы до точки x; l длина конденсатора.

Емкость цилиндрического конденсатора определяется по формуле:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я