1. Главная
  2. Библиотека
  3. Электроника, электротехника, радиотехника
  4. Энергетический спектр гауссовского стационарного случайного процесса  x(t) равен G(w). Среднее значение случайного процесс...

Энергетический спектр гауссовского стационарного случайного процесса  x(t) равен G(w). Среднее значение случайного процесса равно  mx = m1= M{x(t)}. Требуется : 1. Определить корреляционную функцию B(t) случайного процесса.

«Энергетический спектр гауссовского стационарного случайного процесса  x(t) равен G(w). Среднее значение случайного процесса равно  mx = m1= M{x(t)}. Требуется : 1. Определить корреляционную функцию B(t) случайного процесса.»
  • Электроника, электротехника, радиотехника

Условие:

Энергетический спектр гауссовского стационарного случайного процесса  x(t) равен G(w). Среднее значение случайного процесса равно  mx = m1= M{x(t)}.

 Требуется :

1. Определить корреляционную функцию B(t) случайного процесса.

2. Рассчитать величины эффективной ширины спектра и интервала корреляции рассматриваемого процесса.

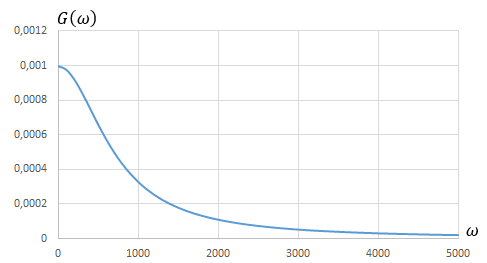
3.  Изобразите графики G(w) и B(t) с указанием масштаба по осям и покажите на них эффективную ширину спектра и интервал корреляции.

4. Запишите выражение для функции плотности вероятности W(x) гауссовского стационарного случайного процесса и постройте её график.


 Исходные данные

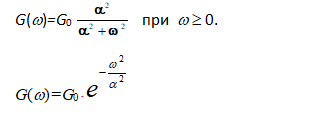
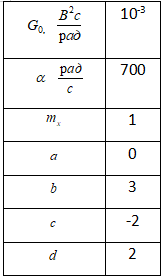
Решение:

Сделаем замену переменной на переменную = - 0 и интегрирование будем производить по переменной на интервале от 0 до .

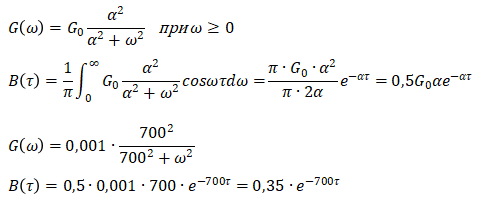
Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я