Условие задачи
На рисунке 1 показана схема цепи с источником периодической несинусоидальной ЭДС. Форма кривой ЭДС е = f(ωt) изображена на рисунке 2. Амплитуда ЭДС Еm, угловая частота ω и параметры цепи даны в таблице 1.
Требуется:
1. Разложить аналитически в ряд Фурье заданную периодическую несинусоидальную ЭДС е=f(ωt), ограничившись вычислением первых трех гармоник. Написать уравнение мгновенного значения ЭДС. Определить действующее значение заданной несинусоидальной ЭДС.
2. Рассчитать три гармоники тока в неразветвленном участке цепи с источником ЭДС. Записать закон изменения этого тока i=f(ωt). Вычислить действующее значение несинусоидального тока.
3. Построить графики первых трех гармоник тока в неразветвленном участке цепи и суммарную кривую тока, полученную в результате графического сложения этих гармоник.
4. Определить активную, реактивную и полную мощности цепи.
5. Рассчитать коэффициент искажения для несинусоидального тока.
Таблица 1 – Исходные данные
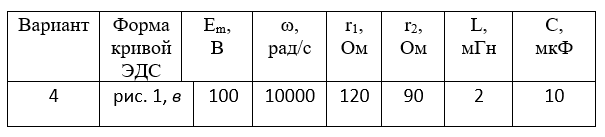
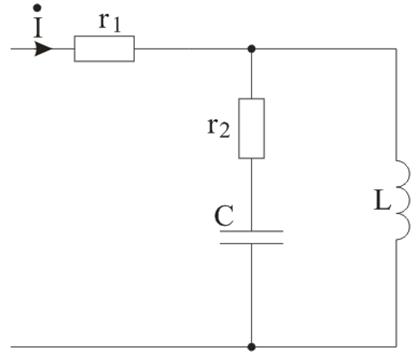
Рисунок 1 – Схема цепи
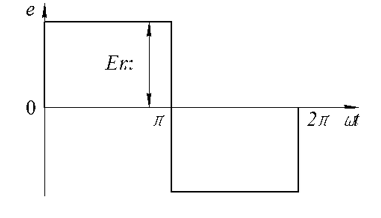
Рисунок 1в – Форма кривой ЭДС
Ответ
1. Разложить аналитически в ряд Фурье заданную периодическую несинусоидальную ЭДС е=f(t), ограничившись вычислением первых трех гармоник. Написать уравнение мгновенного значения ЭДС. Определить действующее значение заданной несинусоидальной ЭДС.
Разложение в ряд Фурье заданной функции е=f(t) с точностью до первых трех гармоник уже известно из условия:
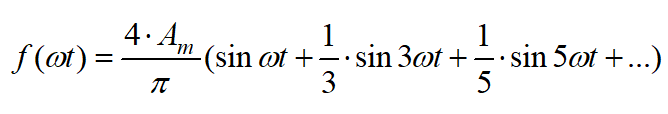
Am это амплитуда заданной функции, равная Em = ...
