Условие:
Две гладкие частицы сферической формы с массами m1 и m2, движущиеся со скоростями 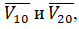 сталкиваются под углом β, как указано на рис.1. Расстояние до места встречи и скорости частиц соответствуют условиям соударения (отсутствию промаха)
сталкиваются под углом β, как указано на рис.1. Расстояние до места встречи и скорости частиц соответствуют условиям соударения (отсутствию промаха)
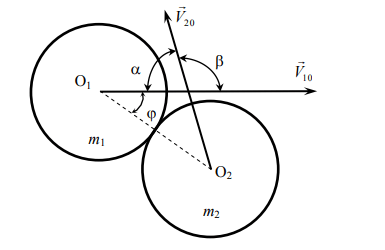
Рис. 1
На рис.1:
β - угол встречи, т.е. угол, образованный векторами 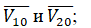
α = (π - β) - дополнительный угол;
φ - угол между линией удара O1O2 и вектором 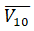
Другие обозначения:
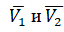 - скорости соответственно 1-ой и 2-ой частицы после удара.
- скорости соответственно 1-ой и 2-ой частицы после удара.
U - совместная скорость частиц после абсолютно неупругого удара.
θ - угол отклонения частицы после удара, т.е. угол, образованный векторами 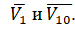
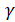 - угол разлета частиц после удара, т.е. угол, образованный векторами
- угол разлета частиц после удара, т.е. угол, образованный векторами 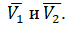
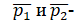 импульсы соответственно 1-ой и 2-ой частицы после удара.
импульсы соответственно 1-ой и 2-ой частицы после удара.
E1, E2 - кинетические энергии соответственно 1-ой и 2-ой частицы после удара.
ΔE - изменение кинетической энергии механической системы, состоящей из двух частиц за время удара.
Виды взаимодействия:
а) абсолютно упругий удар (АУУ);
б) неупругий удар (НУУ);
в) абсолютно неупругий удар (АНУУ).
Общие исходные данные: m* = 10-3 кг, V* = 10 м/с, α* = π/2.

Решение:
При упругом ударе шаров выполняется закон сохранения механической энергии (ЗСМЭ)
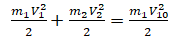
где V10= 3V* начальная скорость 1-го шара,
V1 конечная скорость 1-го шара (скорость 1-го шара после удара),
V2 - конечная скорость 2-го шара (скорость 2-го шара после удара).
Выражение для закона сохранения импульса имеет вид
