Две материальные точки движутся по одной прямой, совпадающей с осью 0x декартовой системы координат. Закон движения первой точки имеет вид x_1 = A + Bt + Ct^2 + Dt^3, а ускорение второй точки изменяется согласно уравнению а_2x = α+βt.
«Две материальные точки движутся по одной прямой, совпадающей с осью 0x декартовой системы координат. Закон движения первой точки имеет вид x_1 = A + Bt + Ct^2 + Dt^3, а ускорение второй точки изменяется согласно уравнению а_2x = α+βt.»
- Физика
Условие:
Две материальные точки движутся по одной прямой, совпадающей с осью 0x декартовой системы координат.
Закон движения первой точки имеет вид x1 = A + Bt + Ct2 + Dt3, а ускорение второй точки изменяется согласно уравнению а2x = α+βt. В начальный момент времени вторая точка имела координату x20 = ɣ и скорость υ20x = δ. Размерности параметров: [A] = м, [B] = м/с, [C] = м/с2, [D] = м/с3.
Определите относительную скорость точек в тот момент, когда их ускорения станут одинаковыми.
Исходные данные:
x1 = A + Bt + Ct2 + Dt3;
а2x = α+βt;
x20 = ɣ;
υ20x = δ;
A=1;
B=7;
С=1;
D=2;
α=8;
β=6;
ɣ=0;
δ=1;
Найти:
s1-2-?
Решение:
При движении координата 1-й точки изменяется по закону
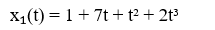
Скорость движения 1-й точки
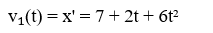
Ускорение движения 1-й точки
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э