Условие:
Две материальные точки движутся согласно параметрическим уравнениям: x1=A1+B1t+C1t2+D1t3 и x2=A2+B2t+C2t2+D2t3. Найти координату, значения скорости и ускорения точек в момент времени t2. Рассчитать средние значения скоростей и ускорений в интервале времени от t2 до t3. Построить графики зависимости x(t),ʋ(t) и a(t) в интервале от t0 до t1 секунд с шагом ∆t =2с. Проверить, возможна ли встреча этих материальных точек (указать по возможности на графике).
Дано:
A1=9
A2=3
B1=-0,6
B2=0,4
C1=0,06
C2=0,04
D1=0,006
D2=0,004
t0=11
t1=21
t2=14
t3=18
Найти:
x(t2)-?
ʋ(t2)-?
a(t2)-?
aср - ?
ʋср - ?
Решение:
Координаты х найдем, подставив в уравнение движения числовые значения коэффициентов A, B, C и D и времени:
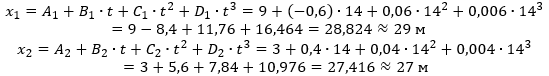
Мгновенная скорость есть первая производная от координаты по времени:
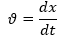
Получаем:
