Две материальные точки движутся согласно уравнениям х1 = A1t + B1t в квадрате + С1t в кубе и х2 = A2t + B2t в квадрате + C2t в кубе где A1 = 8 м/с, B1 = 8 м/с в квадрате; C1= -16 м/с в кубе; A2 = 2 м/с; B2 = -4 м/с в квадрате; С2 = 1 м/с в кубе.
«Две материальные точки движутся согласно уравнениям х1 = A1t + B1t в квадрате + С1t в кубе и х2 = A2t + B2t в квадрате + C2t в кубе где A1 = 8 м/с, B1 = 8 м/с в квадрате; C1= -16 м/с в кубе; A2 = 2 м/с; B2 = -4 м/с в квадрате; С2 = 1 м/с в кубе.»
- Физика
Условие:
Две материальные точки движутся согласно уравнениям х1 = A1t + B1t2 + С1t3 и х2 = A2t + B2t2 + C2t3 где A1 = 8 м/с, B1 = 8 м/с2; C1 = -16 м/с3; A2 = 2 м/с; B2 = -4 м/с2; С2 = 1 м/с3. В какой момент времени t ускорения этих точек будут одинаковыми? Найти скорость v1 и v2 точек в этот момент. Построить графики зависимостей a1(t) и a2(t).
Решение:
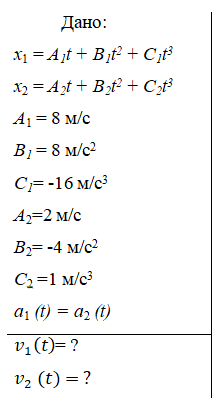
Для одномерного движения вдоль оси ОX, скорость v есть первая производная от координаты по времени, а ускорение a первая производная от скорости по времени или вторая производная от координаты по времени. Найдем скорость и ускорение каждой точки, как функции времени:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э