1. Главная
  2. Библиотека
  3. Физика
  4. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ_1 и σ_2. треб...

На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ_1 и σ_2. требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость Е(r) напряженности электрического

«На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ_1 и σ_2. требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость Е(r) напряженности электрического»
  • Физика

Условие:

На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ1  и σ2. требуется: 1) используя теорему Остроградского-Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II и III.

1) принять σ1=σ,σ2=- σ 

2) вычислить напряженность E в точке, удаленной от центра на расстояние r, и указать направление вектора E, принять σ =0,1 мкКл/м2   ,r=3R 

3) построить график Е(r).

Решение:

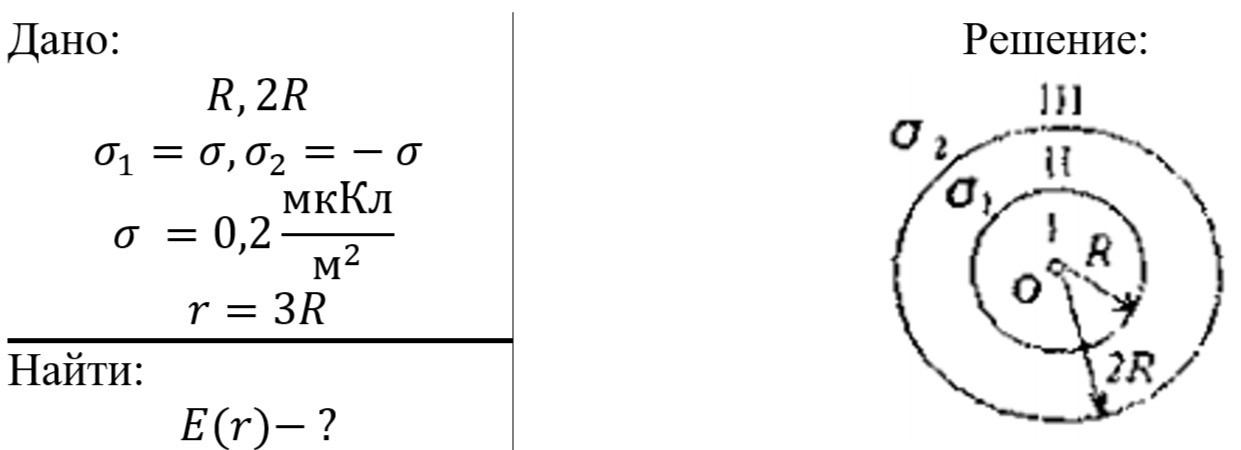
Напряженность электрического поля внутри (r1 R) равномерно заряженной сферы будет равна нулю. Это можно показать, используя теорему Гаусса-Остроградского. Выберем внутри сферы сферическую поверхность радиуса r центр, которой совпадает с центром данной сферы, и рассчитаем поток вектора напряженности через поверхность этой сферы:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я