Условие:
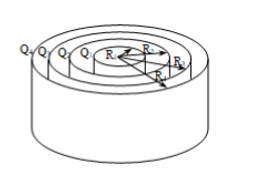
На рисунке приведена система заряженных коаксиальных длинных цилиндров. Радиусы цилиндров R1= 17 см, R2 = 27 см, R3 = 37 см, R4 = 47 см. Линейные плотности зарядов на цилиндрах τ приведены ниже.
1). Постройте график зависимости напряженности электрического поля от расстояния до оси цилиндров.
2). Определите разность потенциалов между внутренним и внешним цилиндрами.
Дано:
R1= 17 см = 0,17 м
R2 = 27 см = 0,27 м
R3 = 37 см = 0,37 м
R4 = 47 см = 0,47 м
τ1 = - 10 нКл/м = - 10-8 Кл/м
τ2 = 20 нКл/м = 2· 10-8 Кл/м
τ3 = - 10 нКл/м = - 10-8 Кл/м
τ4 = 0
Найти:
1) Е(х), 2) Δφ1-4
Решение:
1) По теореме Гаусса поток напряженности E электрического поля через замкнутую поверхность с величиной заряда q внутри этой поверхности, равен
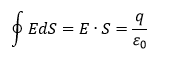
где 0=8,85 ∙10-12 Ф/м - электрическая постоянная.
Пусть этой поверхностью будет цилиндрический контур радиусом r, тогда площадь этой поверхности S=2rl
