Сплошной диск вращается относительно оси, проходящей через его центр масс и перпендикулярной плоскости диска. Уравнения изменения со временем кинематических характеристик вращающегося диска β = Ae-βt. Начальные условия (при t = 0) φ = 0, ω = 0.
- Физика
Условие:
Сплошной диск вращается относительно оси, проходящей через его центр масс и перпендикулярной плоскости диска. Уравнения изменения со временем кинематических характеристик вращающегося диска β = Ae-βt. Начальные условия (при t = 0) φ = 0, ω = 0. Угол поворота φ задан в радианах, А = 0.0314 рад/с2, В = 0.1 рад/с.
1. Построить графики изменения со временем угла поворота φ(t), модуля угловой скорости ω(t) и углового ускорения β(t).
2. Для точки, находящейся на расстоянии R = 0,1 м, определить полное ускорение в момент времени t = 5c.
Решение:
Дано:
А = 0.0314 рад/с2
В = 0.1 рад/с
0 = 0, 0 = 0
t = 5 с
R = 0,1 м
1. построить графики (t), (t), (t).
2. найти а(t =5с)
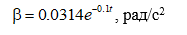
Угловую скорость находим интегрирование с учётом начального условия
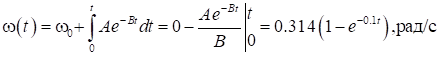
Угол поворота
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства