Условие задачи
Решение малого сфероидического треугольника двумя способами.
Решение треугольника заключается в определении всех его элементов: сторон и углов. Треугольник на поверхности эллипсоида, образованный геодезическими линиями, называют сфероидическим треугольником. Решение такого треугольника с большими длинами сторон с требуемой высокой точностью затруднительно. Треугольник сравнительно малых размеров – со сторонами до 240 километров решается достаточно просто, принимая его за сферический, в котором стороны являются дугами.
Целью работы является решение малых сфероидических треугольников на примере решения треугольника двумя способами:
1. по способу аддитаментов (Зольднер,1820 г.);
2. с использованием теоремы Лежандра (1787 г.).
В геодезии известными обычно являются горизонтальные углы треугольника, измеряемые на пунктах, и длина одной из его сторон. Поэтому задача сводится к нахождению длины двух других сторон треугольника.
Дано:
1) сферический треугольник на поверхности эллипсоида с известной стороной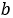 
и сферическими углами:
Таблица 4.1
Значения сферических углов треугольника
Среднее значение широты треугольника В ср. = 55°.
Значение исходной стороны треугольника АС = b принять равным:
где n – последние две цифры шифра студента;
Схема треугольника представлена на рис. 4.1.
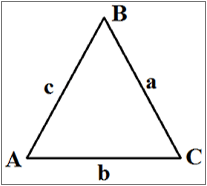
Рис. 4.1 Схема треугольника
Дано:
1) Сферический треугольник на поверхности эллипсоида со стороной:
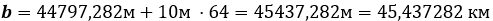
и сферическими углами из таблицы 4.1:
f - коэффициент в функции широты
(для территории РФ при R и b в километрах коэффициент f принимается равным f=0,00253”/ км2).
2) Среднее значение широты треугольника В ср. = 55°.
2.1. Решение малого треугольника по способу аддитаментов
1) Сферический треугольник на поверхности эллипсоида со стороной b и сферическими углами A, B, C, предварительно уравненными за невязку W треугольника:
А, В и С - углы треугольника (значения которых достаточно знать до “;
сторона b – в километрах;
f - коэффициент в функции широты
Если имеется невязка W, то она распределяется поровну в каждый угол:
Ответ
Стороны a, b, c малого треугольника значительно меньше радиуса земного шара R, поэтому, ограничивая разложение синуса малой дуги в ряд только двумя первыми членами, получаем:
где: в скобках длина сторон a, b, c плоского треугольника;
Aa, Bb, Cc аддитаменты (добавки) в длину сферической стороны для получения значения длины стороны плоского треугольника:
