Условие задачи
В некоторый момент времени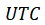 
с пункта земной поверхности P, геодезические координаты ( B, L, H ) которого заданы относительно референц-эллипсоида Красовского с параметрами a и e, определены истинные экваториальные топоцентрические координаты ИСЗ 
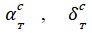и топоцентрическая дальность 
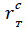до ИСЗ. Предполагается, что при определении истинных экваториальных топоцентрических координат ИСЗ учтены редукционные поправки (прецессия, нутация) за переход от системы координат стандартной эпохи (эпохи каталога J2000.0) к истинной системе координат на эпоху наблюдения (момент наблюдения 
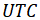– всемирное координированное время).
Предполагается, что синхронным методом решена задача по определению ориентировки (углов Эйлера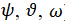 
) референцной (геодезической) системы относительно геоцентрической, а орбитальным методом определены координаты 
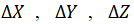центра референц-эллипсоида Красовского относительно центра масс Земли.
Необходимо вычислить геоцентрические экваториальные координаты ИСЗ 
и геоцентрическую дальность 
до ИСЗ.
Исходные данные.
Координаты пункта наблюдения P:
геодезическая широта
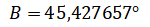
геодезическая долгота
геодезическая высота
Параметры референц-эллипсоида Красовского:
большая полуось
эксцентриситет
Координаты центра референц-эллипсоида Красовского относительно центра масс Земли:
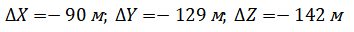
Углы Эйлера:
прецессии
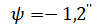
нутации
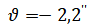
чистого вращения
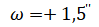
Координаты мгновенного полюса:
Истинные экваториальные топоцентрические координаты ИСЗ и топоцентрическая дальность на эпоху наблюдения:
дальность
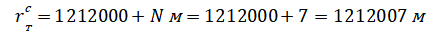
прямое восхождение
склонение
момент наблюдения
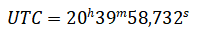
Поправки за переход от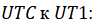 
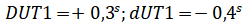
Гринвичское звездное время в полночь на дату наблюдения:
Ответ
1. Длина внутренней нормали к поверхности эллипсоида
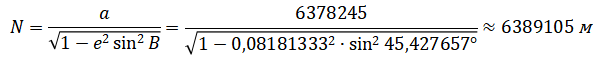
Вычисляем геодезические прямоугольные координаты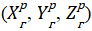 
пункта P в системе референц-эллипсоида Красовского
