На ребрах МВ и МС правильной пирамиды МАВС взяты точки В1 и С1 соответственно - середины этих ребер. Считая боковое ребро пирамиды равным стороне ее основания, найдите угол между плоскостями АВ1С1 и АВС.
- Геометрия
Условие:
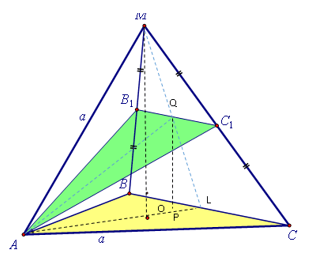
2.7. На ребрах МВ и МС правильной пирамиды МАВС взяты точки В1 и С1 соответственно - середины этих ребер. Считая боковое ребро пирамиды равным стороне ее основания, найдите угол между плоскостями АВ1С1 и АВС.
Решение:
Отрезок B1 C1 средняя линия треугольника AB1C1, следовательно, B1C1∥AB. Значит, через B1C1 можно провести плоскость параллельную плоскости ABC и, так как B1C1AB1 C1 , B1C1 параллельна прямой пересечения плоскостей AB...Cи ABC.Треугольник ABC равнобедренный. Проведем перпендикуляр AQ к , Q середина B C. Из точки Q опустим перпендикуляр QP на плоскость основания. Точка P лежит на AL медиане треугольника ABC, P середина LO. AL BC, следовательно, AL B C и AQ BC. Таким образом, QAP линейный угол искомого угла.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства