Условие:
Привести уравнение кривой второго порядка х2+2у2+ 8у+4=0, к каноническому виду и найти точки пересечения ее с прямой: 5у+4=0
Решение:
Приведем уравнение кривой к каноническому виду:
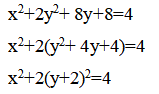
- это эллипс с центром (0;-2) и полуосями

Привести уравнение кривой второго порядка х2+2у2+ 8у+4=0, к каноническому виду и найти точки пересечения ее с прямой: 5у+4=0
Приведем уравнение кривой к каноническому виду:
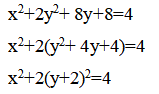
- это эллипс с центром (0;-2) и полуосями
Не нашел нужную задачу?