Вычислить площадь полной поверхности и объём треугольной пирамиды, стороны основания которой равны 13 см, 14 см и 15 см, а боковые грани наклонены к основанию под углом 60 градусов.

Дано:

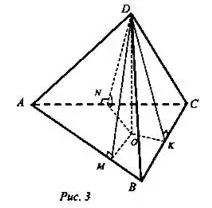
DABC - данная пирамида

DO - высота.

AB=13см; BC=14см; AC=15см

DMO, DKO, DNO - линейные углы двугранных углов боковых граней с плоскостью основания

DMO = DKO = DNO = 45

Найти:

Sполн; V

1.Построим ОМ АВ, ON АС, ОК ВС.

Из теоремы о 3-х перпендикулярах следует, что DM АВ, DK BC, DN AC.

Пусть DMO, DKO, DNO - линейные углы двугранных углов боковых граней с плоскостью основания. По условию DMO = DKO = DNO = 60.

Тогда DMO = DKO = DNO по катету DO и острому углу 600.

из равенства треугольников следует:

МО = OK = ON = r, где r - радиус вписанной в АВС окружности.

DM = DK = DN

2. Рассмотрим треугольник АВС.

...