Вода самотеком перепускается из одного резервуара в другой по трубопроводу. Определить расход при уровнях Н1 и Н2, пренебрегая неустановившемся характером течения и полагая, что в первом приближении режим течения соответствует квадратичной области.

1 августа 2024
Гидравлика

Условие:

Вода самотеком перепускается из одного резервуара в другой по трубопроводу (см. рис.). Определить расход при заданных уровнях Н1 и Н2, пренебрегая неустановившемся характером течения и полагая, что в первом приближении режим течения соответствует квадратичной области с абсолютной эквивалентной зернистой шероховатостью k. Построить диаграмму уравнения Бернулли, а также найти время выравнивания уровней. Геометрические размеры трубопровода даны в таблице, температура воды t = 20⁰C .

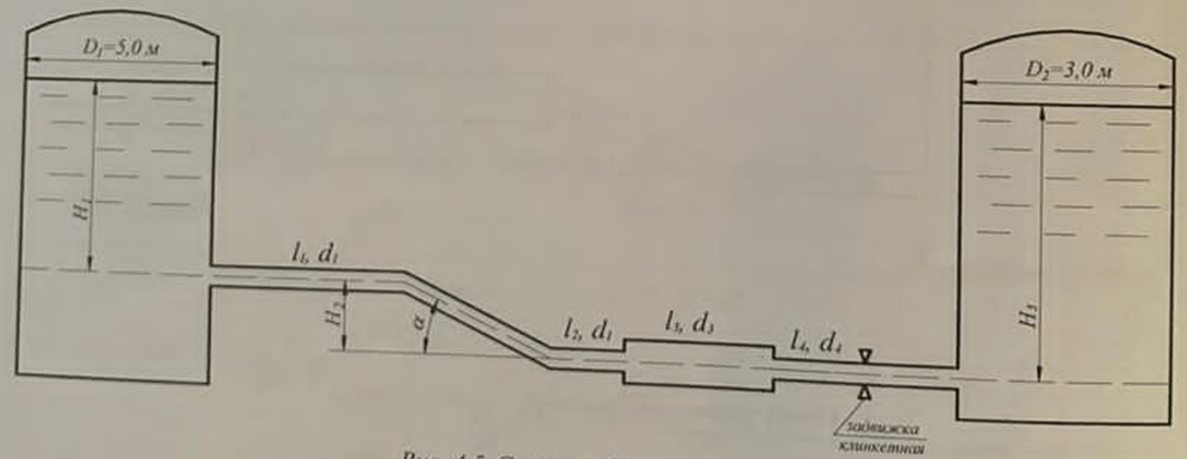
Исходные данные:

L1 = 70 м;

L2 = 10 м;

L3 = 20 м;

L4 = 25 м;

d1 = 100 мм = 0,1 м;

d3 = 200 мм = 0,2 м;

d4 = 150 мм = 0,15 м;

Н1 = 12 м;

Н2 = 5 м;

Н3 = 6 м;

α = 60⁰;

k = 0,3 мм = 3·10^-4м;

t = 20 ⁰C;

D1 = 5 м;

D2 = 3 м.

Q - ? T - ?

Решение:

Из справочных данных: кинематическая вязкость воды при t = 20 ⁰C = 1,00610^-6 м²/с, плотность воды при этой же температуре = 998 кг/м³.

Запишем уравнение Бернулли для двух сечений, совпадающих с уровнями воды в резервуарах. Плоскость сравнения по оси трубопровода (в самой нижней его части).

Z1 + P1/g + 1V1²/2g = Z2 + P2/g + 2V2²/2g + h_w.

Здесь

Z1 = H1 + H2 ; Z2 = H3 ; P1 = P2 ; 1 = 2 = 1 (в предположении турбулентного режима); V1 = V2 = 0; h_w потери напора .

Получим:

H1 + H2 Н3 = h_w.

где

h_w= h_Д + h_М,

где

h_Д потери напора по длинне;

h_М местные потери напора.

Из геометрическ...