Удельный прирост массы образца кобальта (г/см2) со временем описывается квадратно-параболическим уравнением Δm2=3·10-6·exp(-92930/RT)τ, (где τ– время в секундах). Продукт коррозии – СоО. На какую глубину проникнет коррозия за год при t = 300ºС?
«Удельный прирост массы образца кобальта (г/см2) со временем описывается квадратно-параболическим уравнением Δm2=3·10-6·exp(-92930/RT)τ, (где τ– время в секундах). Продукт коррозии – СоО. На какую глубину проникнет коррозия за год при t = 300ºС?»
- Химия
Условие:
Удельный прирост массы образца кобальта (г/см2) со временем описывается квадратно-параболическим уравнением Δm2=3·10-6·exp(-92930/RT)τ, (где τ– время в секундах). Продукт коррозии – СоО. На какую глубину проникнет коррозия за год при t = 300ºС?
Решение:
Допустим, пластинка имеет размеры 11 см. Тогда ее объем будет равен V= 0,01см3, а масса 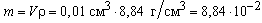 г.
г.
Находим прирост массы образца кобальта (г/см2):
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э