Условие:
Пусть грамматика Хомского определяется правилами:

К какому классу грамматик Хомского она относится? Постройте несколько терминальных цепочек языка, порождаемого этой грамматикой. Попробуйте сформулировать более простую (узкую) эквивалентную грамматику для порождения этого языка.
Отобразите данную грамматику с помощью иного метода задания (БНФ-нотации, язык синтаксических диаграмм, грамматики с рассеянным контекстом)
2. Определите, к какому типу относится данная грамматика, и какой язык порождает (представить в виде регулярного выражения):

3. Допустим, комбинация, открывающая сейф, набирается из алфавита, состоящего из десятичных цифр и заглавных букв латинского алфавита. Каждая комбинация может состоять из четырех символов, причем первый и последний символ не должны совпадать. Постройте регулярную грамматику, обеспечивающую формирование правильных комбинаций.
4. Дана грамматика, определяемая правилами
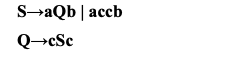
и порожденная терминальная цепочка acacaccbcbcb. Восстановите дерево вывода этой цепочки (правосторонний вывод, восходящий распознаватель)
5. Постройте грамматику, которая позволяет порождать цепочки из 0 или 1 с неравным количеством 0 и 1.
Представьте полученную грамматику в виде блок-схемы алгоритма формирования правильных цепочек языка и эквивалентного конечного автомата.
Промоделируйте работу конечного автомата, убедитесь в корректности его работы на нескольких тестовых последовательностях.
Постройте распознаватели грамматики на основе автомата с магазинной памятью и на базе машины Тьюринга. Промоделируйте работу распознавателей с помощью уже использованных тестовых последовательностей и убедитесь в корректности их работы.
Решение:
1. Грамматика:

Грамматика относится ко классу грамматик Хомского 2 классу контекстно-свободных.
Терминальные цепочки, порождаемые грамматикой:
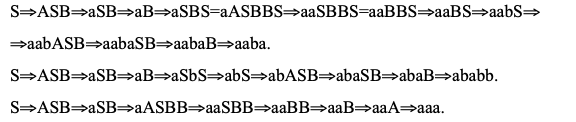
Более простая (узкая) эквивалентная грамматика без нетермин...
