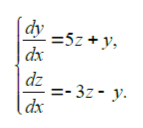
1. Решить данную систему обыкновенных дифференциальных уравнений первого порядка методом Рунге – Кутта при заданных начальных условиях. Начальные условия: при x = 0, y = 1, z = 5 2. Составить программу расчета. Произвести расчет интегральной кривой,

1. Точное решение: 2. Для составления кода программы определим коэффициенты c1, c2 в точных решениях СДУ: отсюда 3. Код программы: program sodu_var6; {вариант 6}вариант 6}uses crt, printer;const n=2; {вариант 6}Количество дифференциальных уравнений}const epsilon=0.0001; {вариант 6}необходимая точность решения - разница между численным и точным}type dim=array[1..n] of real;vary_rk:dim; {вариант 6}массив для хранения результатов Рунге-Кутта y[1] - y, y[2] - z}y_ex:dim; {вариант 6}массив для хранения аналитических результатов}x,h:real; {вариант 6}x-независимая переменная, h-шаг}c1,...