Главная
Библиотека
Информатика
1. Составить математическую модель двойственной задачи к задаче: Для производства двух видов изделий А и B используется тр...

1. Составить математическую модель двойственной задачи к задаче: Для производства двух видов изделий А и B используется три вида сырья. На производство единицы изделия А требуется затратить сырья первого вида a1 кг, сырья второго вида - a2 кг, третьего -

«1. Составить математическую модель двойственной задачи к задаче: Для производства двух видов изделий А и B используется три вида сырья. На производство единицы изделия А требуется затратить сырья первого вида a1 кг, сырья второго вида - a2 кг, третьего -»

17 января 2024
Информатика

Условие:

1. Составить математическую модель двойственной задачи к задаче:

Для производства двух видов изделий А и B используется три вида сырья. На производство единицы изделия А требуется затратить сырья первого вида a1 кг, сырья второго вида - a2 кг, третьего - a3 кг. На производство единицы изделия В требуется затратить сырья первого вида b1 кг, сырья второго вида - b2 кг, третьего - b3 кг. Производство обеспечено сырьем первого вида в количестве t1 кг, второго вида в количестве t2 кг, третьего вида t3 кг. Прибыль от реализации единицы готового изделия А составляет r1 денежных единиц, изделия В - r2 денежных единиц. Составить план выпуска изделий, обеспечивающий максимальную прибыль.

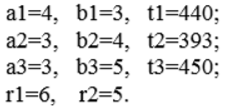
2. Решить прямую и двойственную ЗЛП симплекс-методом.

3. Провести экономико-математический анализ полученных оптимальных решений.

Решение:

Построим двойственную задачу по следующим правилам.

1. Количество переменных в двойственной задаче равно количеству неравенств в исходной.

2. Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной.

3. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи.

Столбец свободных членов исходной задачи является строкой коэффициентов для целевой функции двойственной. Целевая функция в одной задаче максимизируется, в другой минимизируется.

Расширенная матрица A.