Условие:
Дана произвольная последовательность натуральных положительных чисел
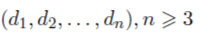
такая, что
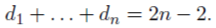
Найдите количество различных деревьев на множестве вершин {1, 2, . . . , n}, у которых вершина 1 имеет степень d1, вершина 2 имеет степень 2, . . . , вершина n имеет степень dn.
Решение:
Последовательности длины n2, состоящие из номеров вершин, однозначно кодируют все различные деревья, причем если вершина v имеет степень dv, то она встречается в этой последовательности ровно dv1 раз.
Тогда наша задача свелась к тому, чтобы посчитать количество последовательностей длины n 2, состоящих из чисел 1, 2, . . . , n, в кото...
