Главная
Библиотека
Информатика
Для заданного алгебраического уравнения Рn(х) = 0 (уравнение составляется по данным таблицы) найти: 1. Общее количество ко...

Для заданного алгебраического уравнения Рn(х) = 0 (уравнение составляется по данным таблицы) найти: 1. Общее количество корней; 2. Количество положительных и отрицательных корней; 3. Предельные оценки и область существования корней; 4. Выделить один

«Для заданного алгебраического уравнения Рn(х) = 0 (уравнение составляется по данным таблицы) найти: 1. Общее количество корней; 2. Количество положительных и отрицательных корней; 3. Предельные оценки и область существования корней; 4. Выделить один»

12 января 2024
Информатика

Условие:

Для заданного алгебраического уравнения Рn(х) = 0 (уравнение составляется по данным таблицы) найти:

1. Общее количество корней;

2. Количество положительных и отрицательных корней;

3. Предельные оценки и область существования корней;

4. Выделить один действительный корень.

5. Используя среду Octave (MATLAB) найти все корни алгебраического уравнения при помощи команды roots.

6. Оценить погрешность значения корня, найденного в п. 4.

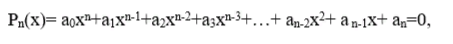
исходные данные для которого следует взять из таблицы , причём степень n полинома левой части Рn(х) уравнения Рn(х)=0 определяется в зависимости от N_д из выражений:

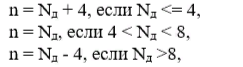
Общее количество корней (задание 1) определить по наивысшей степени полинома в левой части алгебраического уравнения.
Количество положительных и отрицательных (отдельно) корней (задание 2) определить, применяя правило Декарта.
Предельные оценки и область существования корней алгебраического уравнения (задание 3) определить, применяя Метод Лагранжа.
Выделение одного действительного корня (задание 4) произвести по методу уточнения действительно корня (один для всех вариантов метод). Если действительный корень выделить удаётся, то далее снизить порядок исходного алгебраического уравнения на единицу, применяя схему Горнера.
Используя команду roots в среде Octave (MATLAB) найти все значения корней (задание 5).

Решение:

Метод Лагранжа Nд = 4, значит степень полинома равна 8. Eсли коэффициенты полинома удовлетворяют условию то верхняя граница положительных корней уравнения находится по формуле: где m- номер первого отрицательного коэффициента B- наибольший по модулю отрицательный коэффициент уравнения f(x)=0. Согласно методу Лагранжа. Уточняем один корень методом половинного деления. Строим график многочлена: Алгоритм метода следующий: Шаг 1 вычисляем значение функции в середине отрезка Шаг 2 Из двух отрезков и выбираем один, в котором произведение значений функций на концах меньше нуля Т.е...