1. Главная
  2. Библиотека
  3. Информатика
  4. Двумерная выборка результатов совместных измерений признаков икс и игрек объемом н равно 100 измерений. Найти игрек в и ку...

Двумерная выборка результатов совместных измерений признаков икс и игрек объемом н равно 100 измерений. Найти игрек в и ку игрек. Построить уравнение прямой регрессии игрек на икс в виде игрек икс равно аикс плюс б.

«Двумерная выборка результатов совместных измерений признаков икс и игрек объемом н равно 100 измерений. Найти игрек в и ку игрек. Построить уравнение прямой регрессии игрек на икс в виде игрек икс равно аикс плюс б.»
  • Информатика

Условие:

Двумерная выборка результатов совместных измерений признаков x и  y объемом N=100  измерений задана корреляционной таблицей 5.

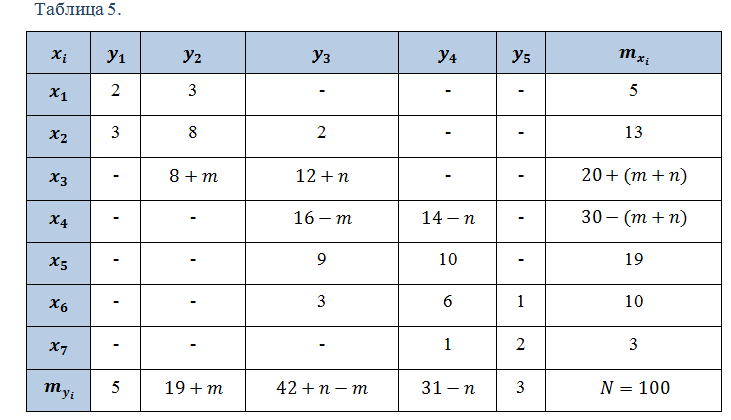
где xi=0,2∙m+(i-1)∙0,3∙n,yj=0,5∙m+(j-1)∙0,2∙n.

Найти 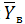и σy для выборки

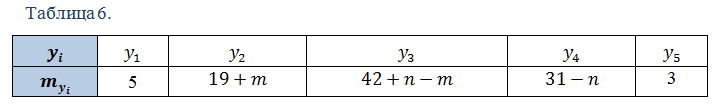
1.   Построить уравнение прямой регрессии Y на X в ви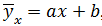де , где 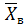= 1,252 и σx = 0,428

2.   На графике изобразить корреляционное поле, то есть нанести точки 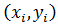и построить прямую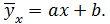

Примечание: Уравнение регрессии сначала рекомендуется найти в виде:

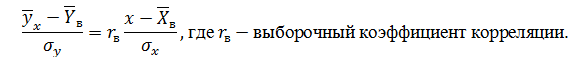
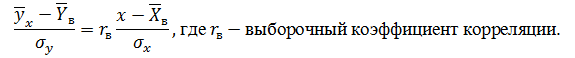
Решение:

Последние цифры шифра 56, соответственно m=2, 𝑛=1.

Тогда:

y1=0,5∙2+(1-1)∙0,2∙1=1+0=1

y2=0,5∙2+(2-1)∙0,2∙1=1+0,2=1,2

y3=0,5∙2+(3-1)∙0,2∙1=1+0,4=1,4

y4=0,5∙2+(4-1)∙0,2∙1=1+0,6=1,6

y5=0,5∙2+(5-1)∙0,2∙1=1+0,8=1,8

my2=19+2=21

my3=42+1-2=41

my4=31-1=30

Таким образом, получили следующую выборку результатов измерений (Таблица 7):

Корреляционная таблица будет иметь следующий вид (Таблица 8):

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я