Каждый рабочий в каждый момент времени может обслуживать не более одного станка, и каждый станок может обслуживаться не более чем одним рабочим. Каждый станок выходит из строя под воздействием простейших потоков за средний интервал.
- Информатика
Условие:
Бригада из X рабочих обслуживает Y станков. Каждый рабочий в каждый момент времени может обслуживать не более одного станка, и каждый станок может обслуживаться не более чем одним рабочим. Каждый станок выходит из строя под воздействием простейших потоков за средний интервал T ̅. Каждый станок восстанавливается под воздействием простейших потоков событий за средний интервал v ̅. Соответственно интенсивности выхода из строя λ=1/T ̅ и восстановления μ=1/v ̅ .
Найти вероятность того, все Y станков находятся в рабочем состоянии. Найти вероятность того, все Y станков находятся в нерабочем состоянии. Найти среднее число неработающий станков m ̅. Сколько из них находится в состоянии ремонта R (среднее число занятых рабочих k ̅) R=k ̅, среднюю длину очереди l ̅ станков на ремонт, коэффициент загрузки каждого рабочего R1, среднее время ожидания станка в очереди на ремонт w ̅, среднее время пребывания станка в неисправном состоянии u ̅.
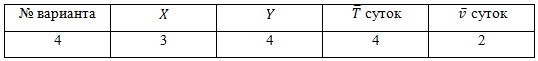
Решение:
Имеем многоканальную СМО замкнутого типа.
Соответствующий граф переходов между состояниями (индекс в обозначении состояния соответствует числу неисправных станков):

Вычисляем нагрузку на СМО:
=/=v ̅/T ̅ =2/4=1/2
Вычисляем вероятность отсутствия заявок в системе по формуле:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства