1. Главная
  2. Библиотека
  3. Информатика
  4. Разработайте алгоритм и программу вычисления точного значения функции.

Разработайте алгоритм и программу вычисления точного значения функции.

«Разработайте алгоритм и программу вычисления точного значения функции.»
  • Информатика

Условие:

Разработайте алгоритм и программу вычисления точного значения функции по формуле  y = sin(x) и ее приближенного значения S, представленного бесконечным рядом 

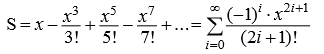
при изменении аргумента функции от  xнач=3,2   до  xкон=4,8  с шагом Δx=0,2. 

Суммирование членов ряда производить до достижения требуемой точности  ε = 0,0001. То есть прибавлять очередной член ряда до тех пор, пока его значение по абсолютной величине не станет меньше ε. Для предотвращения зацикливания предусмотреть завершение процесса суммирования членов ряда по заданному максимальному номеру члена ряда  n =1000. 

Решение:

Решение:

Алгоритм решения предполагает использование двух вложенных друг в друга циклов. Внешний цикл необходим для перебора последовательности значений аргумента x. Для этого цикла выберем структуру с предусловием: начиная с x = xнач проводим повторяющиеся действия (вычисляем точное и приближенное значения функции) с последовательным увеличением x на величину шага x, пока текущее значение x не превысит xкон. Внутренний цикл необходим для вычисления приближенного значения функции, как суммы сходящегося ряда S=b+a0+a1+...+ai+..., где i порядковый номер члена, b постоянный начальный член ряда. ...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я