1. Главная
  2. Библиотека
  3. Информатика
  4. Решить дифференциальное уравнение вида у' = f(х) + ху при за­данных начальных условиях хо = а, у(хо)= у(а) = 0 в заданных...

Решить дифференциальное уравнение вида у' = f(х) + ху при за­данных начальных условиях хо = а, у(хо)= у(а) = 0 в заданных пределах [a, b] с шагом не менее (b - а)/ 10. Выражение f(x) из таблицы. Таблица - Исходные данные 1) Решить дифференциальное

«Решить дифференциальное уравнение вида у' = f(х) + ху при за­данных начальных условиях хо = а, у(хо)= у(а) = 0 в заданных пределах [a, b] с шагом не менее (b - а)/ 10. Выражение f(x) из таблицы. Таблица - Исходные данные 1) Решить дифференциальное»
  • Информатика

Условие:

Решить дифференциальное уравнение вида у' = f(х) + ху при за­данных начальных условиях хо = а, у(хо)= у(а) = 0 в заданных пределах [a, b] с шагом не менее (b - а)/ 10. Выражение f(x) из таблицы. 

Таблица - Исходные данные

1) Решить дифференциальное уравнение методом Эйлера. Построить график y(x).

2) Используя команду Odesolve среды MathCAD вывести значения решения на первых пяти шагах и построить график функции y(x).

3) Используя команду rkfixed среды MathCAD вывести значения решения на первых пяти шагах и построить график функции y(x). 

Сравнить полученные результаты, сделать выводы.

Решение:

Метод Эйлера:

в общем виде задача запишется так

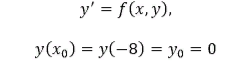
Приближенное решение в узлах xi , которое обозначим через yi, определяется по формуле

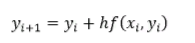
Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я