Условие:
Решить систему линейных уравнений методом обратной матрицы.
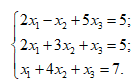
Решение:
В ячейки А2:С4 вводим исходные данные - коэффициенты системы. В ячейки Е2:Е4 вводим свободные члены.
Используя правило умножения матриц, систему можно записать в эквивалентном матричном виде АХ=В, где А заданная матрица; В заданный вектор-столбец, Х неизвестный вектор-столбец.
Решением системы уравнений является такой вектор-столбец Х, который обращает уравнение в тождество. Если определитель D матрицы А отличен от нуля, то система имеет единственное решение, которое можно найти по формулам Крамера и методо...
