Условие задачи
Организация намерена инвестировать часть капитала в ценные бумаги А и В, при этом ожидаемая доходность ценной бумаги А составляет 7%, а среднеквадратическое отклонение доходности составляет 5%; ожидаемая доходность ценной бумаги В – 12%, а среднеквадратическое отклонение доходности – 8%.
1. Определить множество допустимых портфелей и выделить на графике из допустимого множества эффективное подмножество, при значениях коэффициента корреляции +1; с долей ценных бумаг А в портфеле (Х) равной: 1; 0,8; 0,6; 0,4; 0,2; 0.
2. Определить долю ценных бумаг А в портфеле, при которой риск портфеля будет минимальным.
3. Как изменится доля ценных бумаг А в портфеле, при которой риск портфеля будет минимальным, если ожидаемая доходность ценной бумаги А увеличится на 4 процентных пункта?
Ответ
1) Вычислим ожидаемую доходность и среднее квадратическое отклонение портфеля при значениях коэффициента корреляции +1.
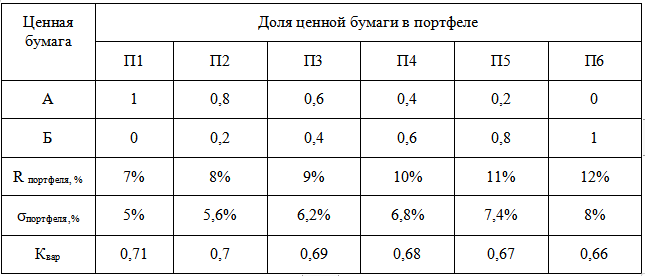
Доходность портфеля составит:
R п1 = 1 7% + 0 12% = 7 %.
R п2 = 0,8 7% + 0,2 12% = 5,6% + 2,4% = 8%.
R п3 = 0,6 7% + 0,4 12% = 4,2% + 4,8% = 9%.
R п4 = 0,4 7% + 0,6 12% = 2,8% + 7,2% = 10%.
R п5 = 0,2 7% + 0,8 12% = 1,4% + 9,6% = 11%.
R п6 = 0 7% + 112% = 12%.
Сре...
