Условие:
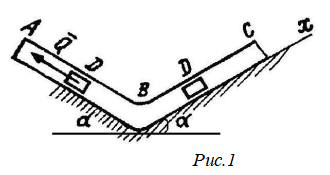
Груз массой m=1,8кг, получив в точке А начальную скорость V0=15м/с, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости.
Участки трубы или оба наклонные, или один – горизонтальный, а другой – наклонный. Угол наклона α = 30°.
На участке АВ на груз кроме силы тяжести действует постоянная сила Q=5Н и сила сопротивления среды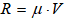 
, зависящая от скорости 
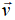груза (направлена против движения), 
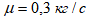. Трением груза о трубу на участке АВ пренебречь.
В точке В груз, не меняя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует сила трения (коэффициент трения f = 0,2) и переменная сила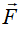 
, проекция которой на ось х: Fx =9t2 Н.
Считая груз материальной точкой и зная время t1=2c движения груза от точки А до точки В, найти закон движения груза на участке ВС, т.е. х =f(t), где х=ВD.
Решение:
Считаем груз материальной точкой.
Рассмотрим движение груза D на участке АВ трубы. Изображаем груз (в произвольном положении) и действующие на него силы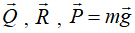 
, реакцию трубы (рис.2). Проводим ось Аz и составляем дифференциальное уравнение в проекции на эту ось: