Условие задачи
Дано: рисунок Д4.4;
R4=0.3 м; r4=0.1 м; R5=0.2 м; r5=0.1 м;
m1=6 кг; m2=0; m3=2 кг; m4=0; m5=8 кг;
М4=0.6 Нм; f=0.1;
F=20(5+2s); s1=1.2 м.
Найти: ω5.
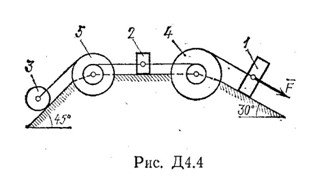
Механическая система состоит из грузов 1 и 2, цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R4 = 0,3 м, r4 = 0,1 м, R5 = 0,2 м, r5 = 0,1 м (массу каждого шкива считать распределенной по внешнему ободу).
Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям (коэффициент трения скольжения грузов о плоскости f = 0,1).
Под действием постоянной силы F система приводится в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивления, равные соответственно М4 и М5.
Для рассматриваемой механической системы составить уравнение Лагранжа второго рода и определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы F равно s1.
Ответ
1. Система имеет одну степень свободы. Выберем в качестве обобщенной координаты перемещение груза 1, полагая, что груз движется по направлению силы F.
Составим уравнение Лагранжа
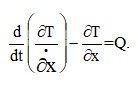
2. Определим кинетическую энергию Т системы, равную сумме энергий всех тел:
Т=Т1+Т2+Т3+Т4+Т5.
Скорости выразим через скорость тела 1.
Для груза 1:
