1. Главная
  2. Библиотека
  3. Механика
  4. Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течении τ с. Ег...

Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течении τ с. Его начальная скорость VA. Коэффициент трения скольжения тела по плоскости равен f.

«Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течении τ с. Его начальная скорость VA. Коэффициент трения скольжения тела по плоскости равен f.»
  • Механика

Условие:

Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течении τ с. Его начальная скорость VA. Коэффициент трения скольжения тела по плоскости равен f. В точке В тело покидает плоскость со скоростью VB, описывая траекторию y=f(x) и попадает в точку С плоскости ВС или ВD со скоростью VC, находясь в полёте Т с. Считать α = 30° и β = 60°. При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.

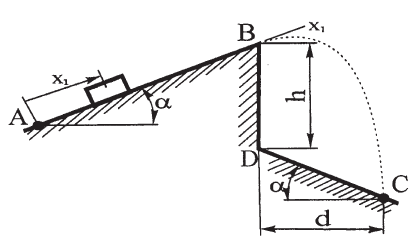
Решение:

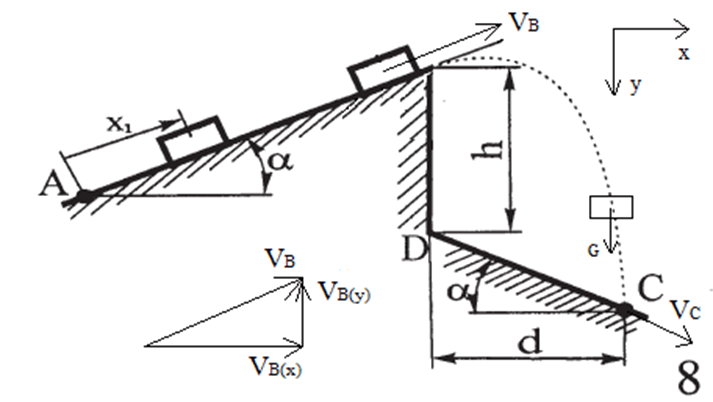
Для нахождения необходимых величин достаточно рассмотреть только участок BC.

Рассмотрим движение груза на участке ВС: скорость VВ будет для движения на этом участке начальной скоростью (Vo = VB). Изображаем груз (в произвольном положении) и действующую на него силу тяжести G=mg. Проводим из точки В оси Вх и Ву и составим дифференциальные уравнения движения тела

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я