1. Главная
  2. Библиотека
  3. Механика
  4. Требуется: определить положение центра тяжести сечения; вычислить моменты инерции относительно двух взаимно перпендикулярн...

Требуется: определить положение центра тяжести сечения; вычислить моменты инерции относительно двух взаимно перпендикулярных центральных осей; установить положение главных центральных осей инерции; вычислить главные радиусы инерции.

«Требуется: определить положение центра тяжести сечения; вычислить моменты инерции относительно двух взаимно перпендикулярных центральных осей; установить положение главных центральных осей инерции; вычислить главные радиусы инерции.»
  • Механика

Условие:

Дано:

Схема,  а = 11 см.

Требуется:

1.   Определить положение центра  тяжести  сечения. 

2.   Вычислить  моменты  инерции  относительно  двух  взаимно перпендикуляр-ных центральных осей (одна из которых является осью симметрии).  

3.   Установить положение главных центральных осей инерции.  

4.   Вычислить главные радиусы инерции. 

5.   Определить  моменты  сопротивления  сечения  для  нижних, верхних, правых и левых волокон.

                                     

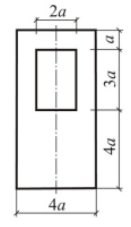
                                              Схема

Решение:

Выбираем начальные координатные оси ОХ0 и ОY0.

Cечение имеет ось симметрии ОY0, следовательно абсцисса центра тяжести сечения равна: ХС = 0. Находим площади составных частей сечения:

2а = 211 = 22 см, 3а = 311 = 33 см, 4а = 411 = 44 см, 8а = 811 = 88 см

Прямоугольника 1: А1 = 4а8а = 4488 = 3872 см2

Прямоугольника 2: А2 = 2а3а = 2233 = 726 см2, (площадь - отрицательная)

Общая площадь сечения: А = А1 - А2 = 3872 - 726 = 3146 см2.

Ординаты ЦТ отдельных частей равны:

уС1 = 4а = 44 см, уС2 = 5,5а = 5,511 = 60,5 см

Ординату центра тяжести сечения определим по формул:

УС = ( А1уС1 - А2уС2)/А = (38...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я