1. Главная
  2. Библиотека
  3. Метрология
  4. Обработка результатов равноточных многократных измерений. 1. Определить основные статистические показатели. 2. Построить г...

Обработка результатов равноточных многократных измерений. 1. Определить основные статистические показатели. 2. Построить гистограмму.

«Обработка результатов равноточных многократных измерений. 1. Определить основные статистические показатели. 2. Построить гистограмму.»
  • Метрология

Условие:

Обработка результатов равноточных многократных измерений.

1. Определить основные статистические показатели. 

2. Построить гистограмму. 

3. Построить теоретическую кривую нормального распределения на том же графике. 

4. Определить доверительный интервал рассеивания случайных погрешностей вокруг среднего значения. 

5. Определить суммарную погрешность обработки. 

6. Ответить на вопросы: Для чего необходимо строить на одном графике теоретическую кривую нормального распределения и гистограмму? Какие выводы можно сделать по данному графику?

Обработка результатов равноточных многократных измерений с получением среднего арифметического , среднеквадратичного отклонения Sx, и определением суммарной погрешности измерения в виде доверительного интервала ± ∑∆Pд.

Исходные данные:

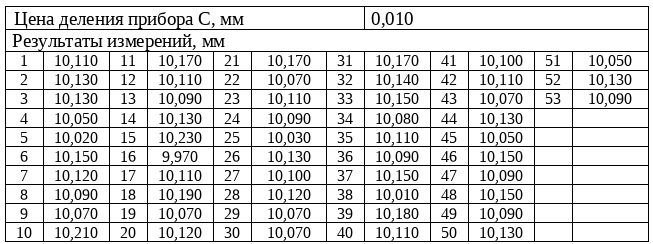
Доверительная вероятность Рд = 0,92 – показывает вероятность нахождения истинного значения в рассчитанном интервале.

Уровень значимости q = 0,02 – показывающий, что принятый закон рассеивания размеров не будет соответствовать реальному закону.

 

Решение:

1. Построение гистограммы.

Определяем величину размаха R (поле рассеяния):

R = Xmax Xmin=10,23-9,97=0,26 мм.

Xmax = 10,23 мм наибольшее из измеренных значений;

Xmin = 9,97 мм наименьшее из измеренных значений.

Определяем число интервалов разбиения n, в соответствии с рекомендациями:

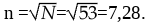
Количество интервалов принимается ближайшим большим нечетным.

Принимаем n = 7.

Опре...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я