1. Главная
  2. Библиотека
  3. Метрология
  4. По известной расчётной зависимости косвенного метода измерения и по результатам и погрешностям прямых измерений, рассчитат...

По известной расчётной зависимости косвенного метода измерения и по результатам и погрешностям прямых измерений, рассчитать предельные и среднеквадратические оценки абсолютной и относительной погрешностей косвенного измерения.

«По известной расчётной зависимости косвенного метода измерения и по результатам и погрешностям прямых измерений, рассчитать предельные и среднеквадратические оценки абсолютной и относительной погрешностей косвенного измерения.»
  • Метрология

Условие:

По известной расчётной зависимости косвенного метода измерения и по известным результатам и погрешностям прямых измерений, в соответствии с полученным вариантом, рассчитать предельные и среднеквадратические оценки абсолютной и относительной погрешностей косвенного измерения

y=(2 ∙ a ∙ b3) / (c + d - e)

∆a = 1;  a = 100

∆b = 2;  b = 80

∆c = 1;   c = 60

∆d = 2;  d = 40

∆e = 1;   e = 20

Решение:

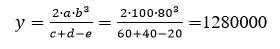
Введём обозначение A=c+d-e тогда y=(2 ∙ a ∙ b3)/A.

Прологарифмируем левую и правую части заданной зависимости

ln⁡y=ln⁡2+ln⁡a+lnb3-lnA.

Найдём дифференциал правой и левой частей

d ln⁡y=dln⁡2+d ln⁡a+3dln⁡b-d ln⁡A.

Так как d ln⁡2=0, получим:

d ln⁡y=d ln⁡a+3dln⁡b-d ln⁡A.

Учитывая, что дифференциал от логарифма переменной величины находится по формуле

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я