Решение задачи
Погрешность измерения расхода расходомером распределена по нормальному закону. Систематическая погрешность равна 0, а СКО результатов измерения составляет 5м3 /час. Определите вероятность того, что результат измерения отличается от истинного
- Метрология
Условие:
Погрешность измерения расхода расходомером распределена по нормальному закону. Систематическая погрешность равна 0, а СКО результатов измерения составляет 5 м3/час.
Определите вероятность того, что результат измерения отличается от истинного значения мощности более чем на Δ1= 45 м3/час и Δ2=55 м3/час?
Таблица А.1
Значения функции Лапласа Ф(х)
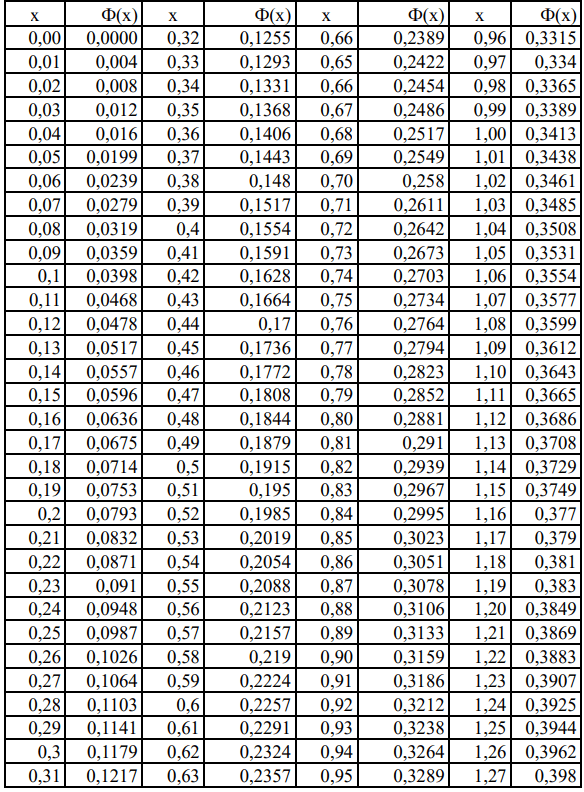
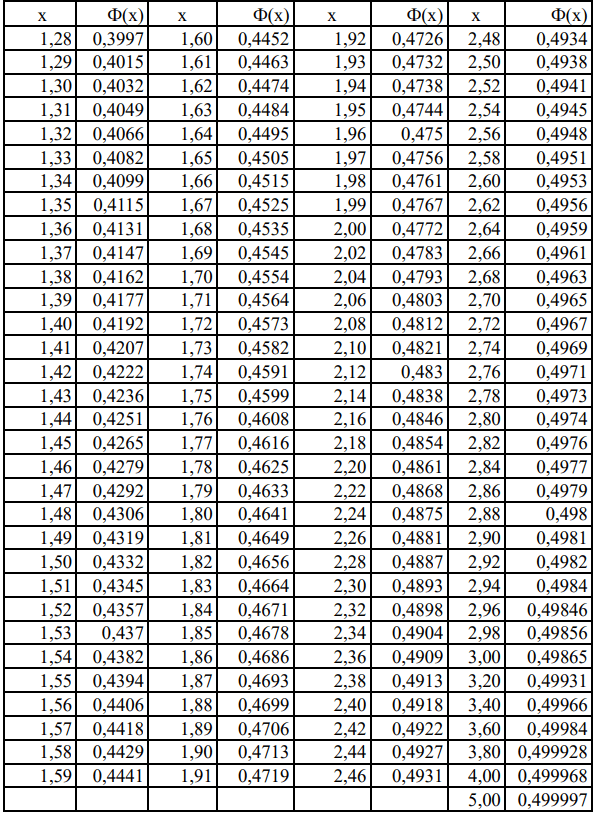
Решение:
Вероятность попадания единичного результата измерения в доверительный интервал Р определяют по
формуле
Рд = Р [U tp* Uи U tp*] = {Ф [(tp)] - Ф [tp]}=2Ф [tp] -1
Значение tP выражаем из формулы доверительного интервала:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э