Условие:
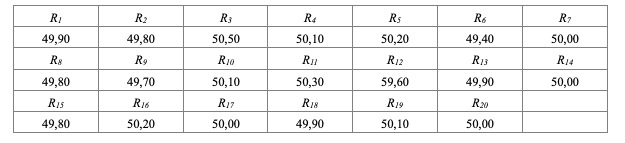
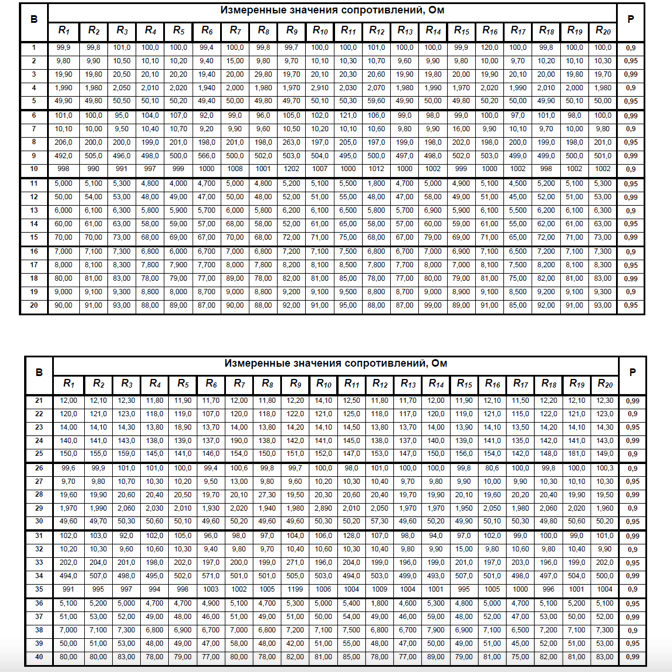
С помощью моста постоянного тока произведено 20 равноточных измерений сопротивления резистора Ri. Данные для своего варианта взять в табл. 1. Систематические погрешности в приведенном ряду отсутствуют, а случайные погрешности распределены по нормальному закону (закону Гаусса).
Требуется выполнить обработку результатов многократных равноточных измерений:
1. Вычислить среднее арифметическое значение ряда отдельных измерений RСР (Ом) (математическое ожидание, результат измерения).
2. Рассчитать среднюю квадратическую погрешность (Ом) результатов единичных измерений в данном ряду.
4. Проверить исходные данные на наличие грубых погрешностей (промахов). В случае их обнаружения исключить результаты измерения с грубой погрешностью, и провести вновь
расчет для нового значения числа измерений n'=n–m (где n = 20, m – количество промахов) начиная с п. 1.
5. Рассчитать среднюю квадратическую погрешность (Ом) среднего арифметического.
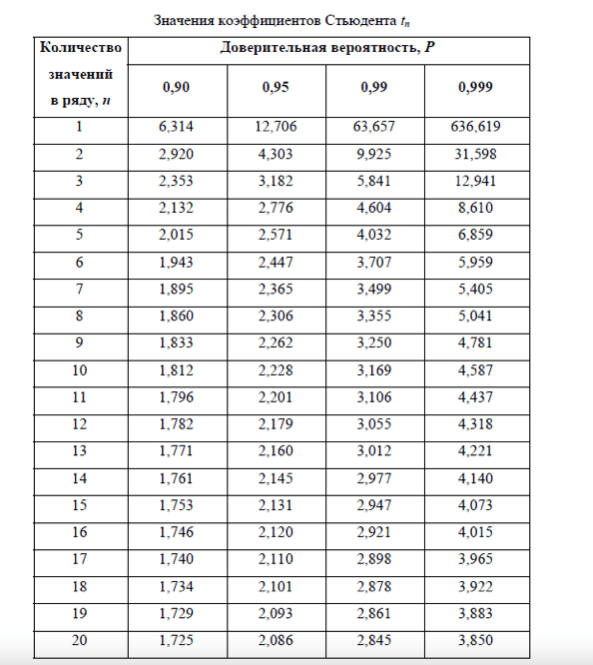
6. Рассчитать доверительный интервал ±∆R (Ом) (∆R= S*tn(n,Р)) при заданной доверительной вероятности Р (табл. 1). Коэффициент Стьюдента tn(n, P) взять из справочных данных (табл. 2) по заданной доверительной вероятности Р и числу измерений n.
7. Записать результат измерения в виде:
R=RCP ± ∆R (Ом), при P = (значение из табл. 1).
8. Проверить результаты измерений на нормальность распределения двумя способами: аналитическим (по составному критерию) и графическим.
Построить для ряда результатов, не содержащего промахов, гистограмму распределения остаточных (случайных) погрешностей, взяв ширину интервалов = 0,5σ.
В этой же системе координат, для сравнения, построить кривую распределения плотности вероятности по нормальному закону.
Примечание: при построении графиков используются значения, полученные после исключения промахов.
9. Сделать вывод о соответствии реального закона распределения случайной погрешности (представленного в виде гистограммы) нормальному закону распределения (закону Гаусса) при числе измерений n ≤ 20.
Исходные данные
Доверительная вероятность Р = 0,95
Таблица 1 – Измеренные значения сопротивления, Ом.
Указания по выполнению задания:
Решение задачи выполняется в последовательности, указанной в задании. Расчеты по пунктам 1, 2, 3, 4 следует повторять столько раз, сколько необходимо для устранения всех промахов из исходного ряда измерений (в некоторых вариантах задания промахов может и не быть).
Пункты 5, 6, 7, 8 выполняются для ряда результатов измерений, не содержащего промахов (с исключенными промахами).
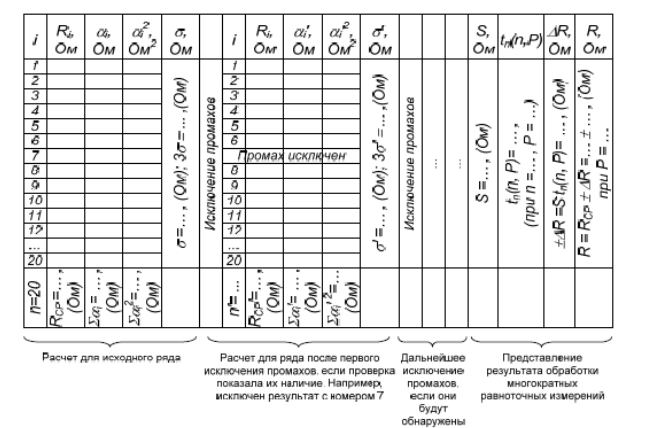
При выполнении каждого пункта задания необходимо записать расчетные формулы в общем виде, с подстановкой чисел, затем вычисленный результат с указанием размерности. При вычислении нескольких результатов по одной формуле приводится пример расчета первого значения, остальные результаты заносятся в табл. 3.
В пункте 8 осуществляется проверка гипотезы о возможности описания распределения случайных погрешностей в обрабатываемом ряду законом Гаусса. С этой целью в одной системе координат строится гистограмма распределения и график закона Гаусса для рассчитанного значения σ.
При построении гистограммы на горизонтальной оси отмечаются интервалы с шириной 0,5σ в пределах от –3σ до +3σ (по 6 интервалов в сторону положительных и отрицательных значений). После вычисления граничных значений всех интервалов выполняют сравнение с ними значений остаточных погрешностей, определяя, в какой из интервалов входит конкретная i-ая погрешность.
После распределения всех остаточных погрешностей по интервалам считают количество вхождений остаточных погрешностей в каждый интервал nj. Если значение точно совпадает с граничным значением, то его включают в один из граничащих интервалов. Для проверки того, все ли остаточные погрешности распределены по интервалам, можно вычислить сумму nj, которая должна равняться количеству измерений в ряду. После определения nj для каждого интервала определяют значения nj / n, по которым для каждого интервала гистограммы изображается прямоугольник с рассчитанной высотой (nj / n).
Значения плотности вероятности по закону Гаусса рассчитываются по выражению (1), в которое в качестве параметра подставляется значение σ, а в качестве переменной – значения ∆ (целесообразно выбрать ∆, равные граничным значениям интервалов).
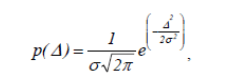

Для удобства построения графиков, рассчитанные значения для гистограммы и закона Гаусса следует занести в табл. 4.
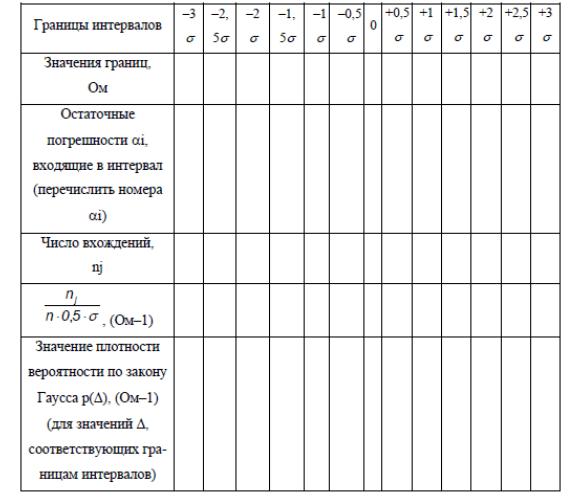
Пример построения гистограммы и графика закона распределения Гаусса:
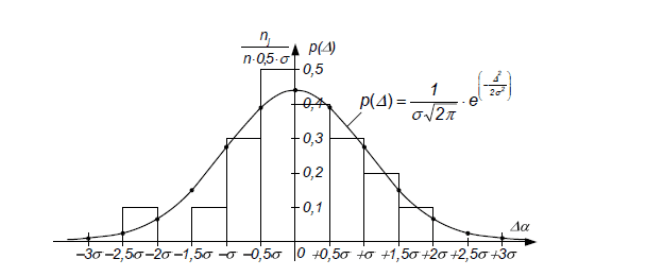
В пункте 9 на основании анализа построенных графиков необходимо сделать вывод о допустимости представления (аппроксимации) закона распределения случайной погрешности законом Гаусса в условиях ограниченного числа измерений в ряду.
Решение:
Заполним следующую таблицу.
Таблица 2 Расчетная таблица
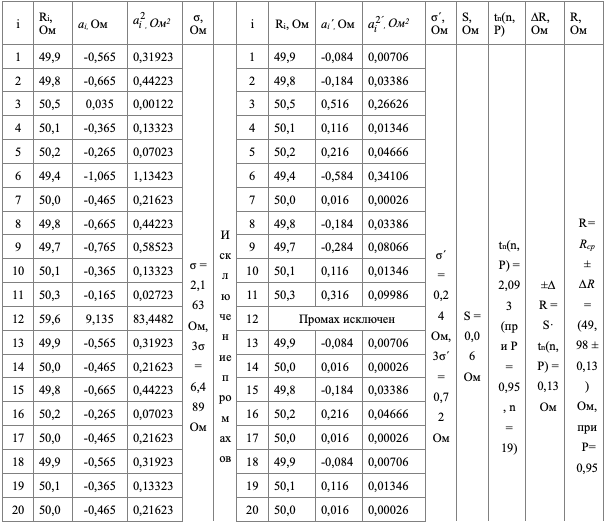

1. Вычислим среднее арифметическое значение ряда отдельных измерений RСР (Ом)
(математическое ожидание, результат измерения):
