1. Главная
  2. Библиотека
  3. Процессы и аппараты
  4. С учетом дифференциальной функции распределения частиц по времени пребывания Е(τ) рассчитать среднюю конечную концентрацию...

С учетом дифференциальной функции распределения частиц по времени пребывания Е(τ) рассчитать среднюю конечную концентрацию и среднюю степень превращения

«С учетом дифференциальной функции распределения частиц по времени пребывания Е(τ) рассчитать среднюю конечную концентрацию и среднюю степень превращения»
  • Процессы и аппараты

Условие:

С учетом дифференциальной функции распределения частиц по времени пребывания Е(τ) рассчитать среднюю конечную концентрацию и среднюю степень превращения, если действительное время пребывания в реакторе совпадает с действительным временем в опытах с трассером. 

В реальном реакторе проводится жидкофазная необратимая реакция, константа скорости k=0,055 С-1 , первый порядок реакции, изменением плотности реакционной смеси  e =-0,1662, СА0=0,2 кмоль/м3.

Решение:

Выражение для определения средней концентрации с использованием функции распределения имеет вид:

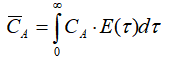
Характеристическое уравнение, определяющее концентрацию реагента для необратимой реакции первого порядка с изменением реакционного объема, имеет вид:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я