1. В результате эксперимента установлено, что в среднем на 100 сообщений длиной 5 символов символ A встречается 50 раз, символ B – 40 раз.
- Программирование
Условие:
1. В результате эксперимента установлено, что в среднем на 100 сообщений длиной 5 символов символ A встречается 50 раз, символ B – 40 раз. Совместно символы A и B встречаются 10 раз. Вычислить условные энтропии
H(A|B) и H(B | А).
2. Определить общую условную энтропию сообщений, составленных из алфавита A, B, если вероятности появления символов в сообщении равны 9 p(A) = 0.6, p(B) = 0.4. Условные вероятности переходов одного символа в другой равны
p(B | A) = 0.15, p(A | B) = 0.1.
3. Сообщения передаются двоичным кодом. В первом случае вероятности появления 0 и 1 равны соответственно p(0) = 0.8 и p(1) = 0.2. Помехи в канале связи отсутствуют, т.е. условные вероятности переходов 0 в 1 и 1 в 0 равны нулю. Во втором случае символы передаются с равными вероятностями p(0)=p(1) = 0.5, однако в результате действия помех условные вероятности переходов равны
p(1 | 1) = 0.8, p(1 | 0) = 0.2, p(0 | 0) = 0.8, p(0 | 1) = 0.2. Чему равна энтропия сообщений в первом и втором случае.
Решение:
1. Определим вероятность появления символа А
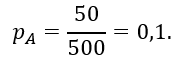
Определим вероятность появления символа B
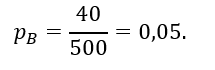
Определим вероятность совместного появления символов А и В
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства