Производственное объединение в своём составе имеет n филиалов Аi, i=1, 2,…, n, которые производят однородную продукцию в количестве аi, i=1, 2,…, n.
- Программирование
Условие:
Производственное объединение в своём составе имеет n филиалов Аi, i=1, 2,…, n, которые производят однородную продукцию в количестве аi, i=1, 2,…, n. Эту продукцию получают m потребителей Bj, j=1, 2, …, m, расположенных в разных местах. Их потребности соответственно равны bj, j=1, 2, …, m. Тарифы перевозок единицы продукции от каждого из филиалов потребителям задаются матрицей Сij (i=1, 2,…, n; j=1, 2, …, m).
Составить план прикрепления получателей продукции к ее поставщикам, при котором общая стоимость перевозок была минимальной.
1. Построить математическую модель задачи.
2. Создать на рабочем листе Excel таблицу для ввода исходных данных.
3. Заполнить таблицу исходными данными и необходимыми формулами.
4. Найти решение задачи средствами надстройки Поиск решения.
5. Вывести отчеты по результатам и устойчивости.
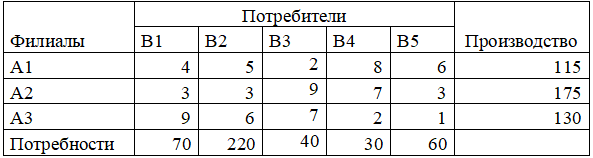
Решение:
1. Построить математическую модель задачи.
xij - поставки из i-го филиала j-ому потребителю.
Целевая функция
4x11 + 5x12+ 2x13 + 8x14 + 6x15 +3x21 + 3x22+ 9x23 + 7x24 + 3x25 +9x31 + 6x32+ 7x33 + 2x34 + x235 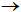 min
min
Ограничения
4x11 + 5x12+ 2x13 + 8x14 + 6x15 = 115
3x21 + 3x22+ 9x23 + 7x24 + 3x25 = 175
9x31 + 6x32+ 7x33 + 2x34 + x235 = 130
4x11 +...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства