Рассчитать оптимальный шаг для построения таблицы значений функции, которая позволит с наименьшей погрешностью вычислить значения
- Программирование
Условие:
1. Рассчитать оптимальный шаг для построения таблицы значений функции, которая позволит с наименьшей погрешностью вычислить значения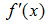 по приближенной формуле центральной разностной производной, если табличные значения функции вычислены с точностью 0.0001.
по приближенной формуле центральной разностной производной, если табличные значения функции вычислены с точностью 0.0001.
2. Найти погрешность, с которой можно найти 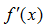 с вычисленным в пункте a) оптимальным шагом.
с вычисленным в пункте a) оптимальным шагом.
3. Написать программу, которая
а) выводит таблицу значений функции с рассчитанным оптимальным шагом h на интервале [c-h, c+16h] (таблица должна содержать 2 столбца: значения аргумента и соответствующее ему округленное до 0.0001 значение функции);
б) По составленной таблице вычисляет приближенные значения 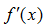 в точках
в точках по формуле центральной разностной производной;
по формуле центральной разностной производной;
в) выводит таблицу точных и приближенных значений производной (таблица должна содержать 3 столбца: значения xi из пункта б) и соответствующие им приближенные и точные значения производной).
В качестве функции взять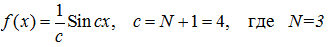
Решение:
Рассчитаем оптимальный шаг дифференцирования для приближенной формулы центральной разностной производной функции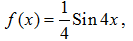 если значения функции с точностью 0.0001.
если значения функции с точностью 0.0001.
Известно, что оптимальный шаг для приближенной формулы центральной разностной производной оценивается по следующему равенству:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства